filmov
tv
Solving x+y=(x-y)^2, a Diophantine Equation

Показать описание
If you need to post a picture of your solution or idea:
#NumberTheoryProblems #DiophantineEquations
PLAYLISTS 🎵 :
#NumberTheoryProblems #DiophantineEquations
PLAYLISTS 🎵 :
Solving x+y=(x-y)^2, a Diophantine Equation
A Diophantine Equation | x^2-y^2=23
A Diophantine Equation (x^2-xy+y^2=x+y)
Solving a Diophantine Equation (3^x-2^y=1)
Cool Trick for Solving the Diophantine Equation (x+y)^2=x^3+y^3 | Integer Solution | Math Olympiad
Diophantine Equation | x+xy+y=54
xy+2x=11 | A Diophantine Equation
Australian Math Olympiad | Diophantine Equation | Algebra | 1/x+1/y=2/35 | Find min(x+y)
A Quadratic Diophantine Equation | Math Olympiads
Can you solve this Systems of Diophantine Equations? 𝑥𝑦+𝑦𝑧=63 and 𝑥𝑧 + 𝑦𝑧 = 23...
A Diophantine Equation | x^y=y^x
Solving x^2+xy+y^2=x^2y^2
A Nice Diophantine Equation in Number Theory | You Should Learn This Theorem | Math Olympiad
A Nice Problem of Number Theory | Diophantine Equation | XY = X + Y + 3 then find integers X and Y
Solving the differential equation xy'+2y=x^3
Solve system of equations: x + y = 2, xy - z^2 = 1. Algebra challenge. Math Olympiad question.
Solving dy/dx=(x-y)/(x+y)
A Diophantine Equation x^2 xy+y^2=x+y
Solving a Nice Math Olympiad Like Diophantine Equation | 2^x+1=y^2
Diophantine Equations: Strategies and Examples
Diophantine Equation | x^y - y^x = 17
5 simple unsolvable equations
If x+y=4 and xy=2, find x^4 + y^4.
How will You find (x ,y )=??? | Math Logic to Solve This Equation | Equation Solving
Комментарии
 0:10:57
0:10:57
 0:00:55
0:00:55
 0:15:44
0:15:44
 0:07:41
0:07:41
 0:03:51
0:03:51
 0:05:12
0:05:12
 0:00:54
0:00:54
 0:06:57
0:06:57
 0:10:19
0:10:19
 0:03:33
0:03:33
 0:00:56
0:00:56
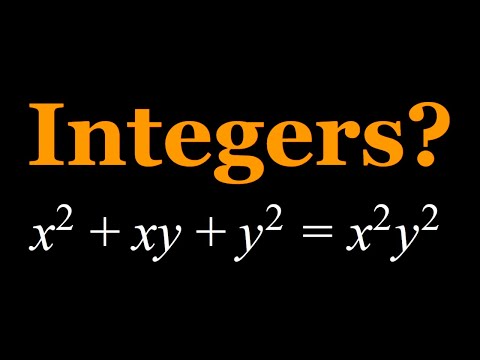 0:07:34
0:07:34
 0:07:40
0:07:40
 0:04:44
0:04:44
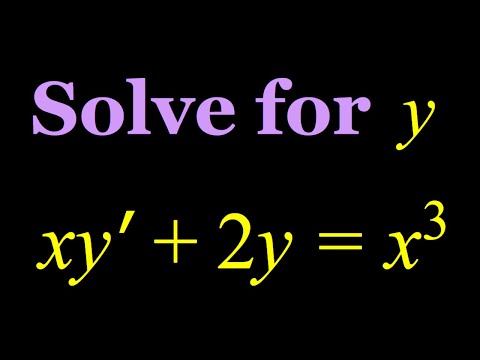 0:08:16
0:08:16
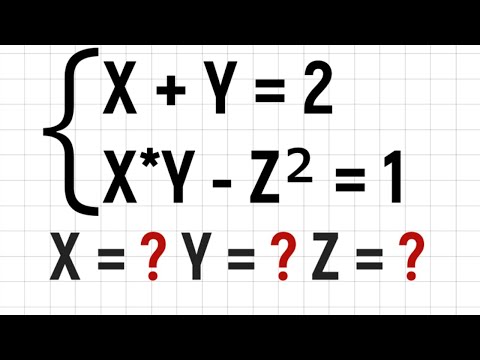 0:01:20
0:01:20
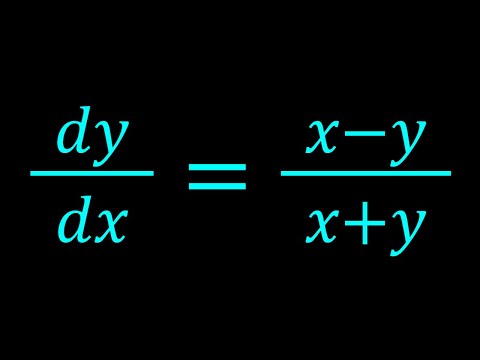 0:09:35
0:09:35
 0:15:44
0:15:44
 0:04:07
0:04:07
 0:27:34
0:27:34
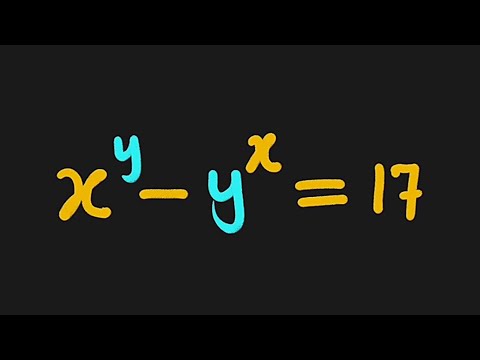 0:08:15
0:08:15
 0:00:50
0:00:50
 0:01:35
0:01:35
 0:04:38
0:04:38