filmov
tv
Solving the differential equation xy'+2y=x^3
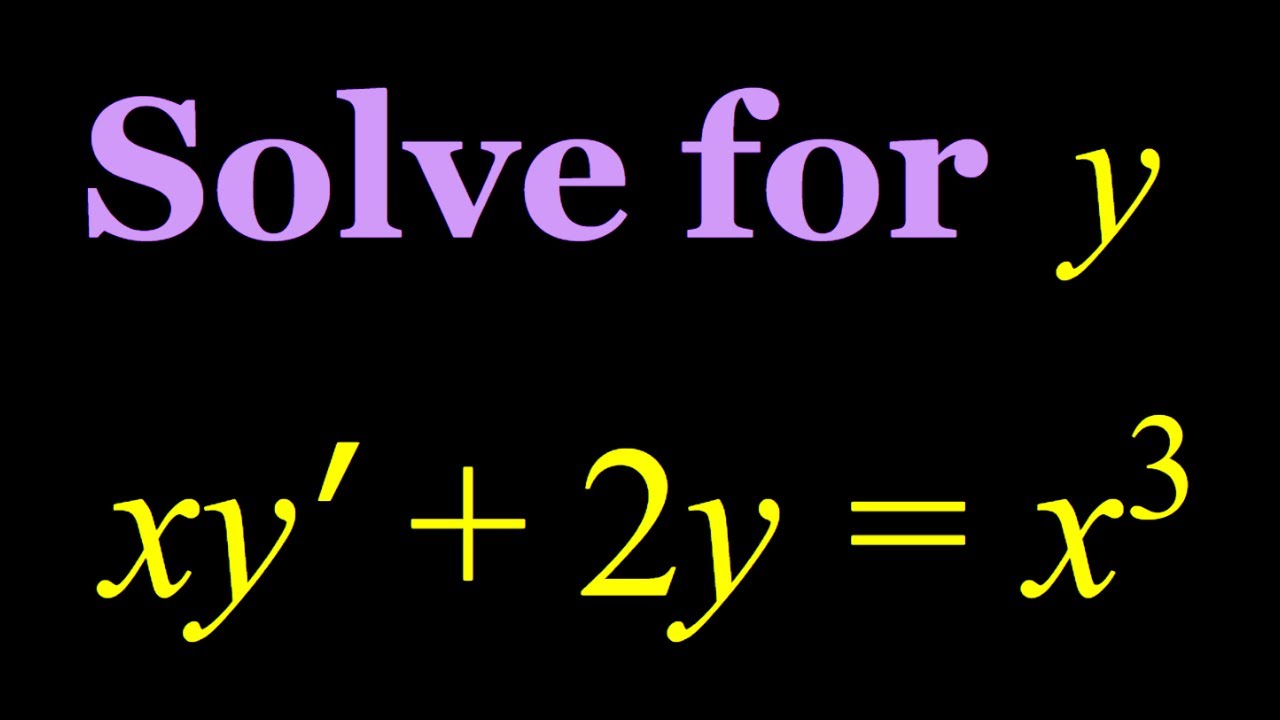
Показать описание
If you need to post a picture of your solution or idea:
#ChallengingMathProblems #FunctionalEquations
EXPLORE 😎:
PLAYLISTS 🎵 :
#ChallengingMathProblems #FunctionalEquations
EXPLORE 😎:
PLAYLISTS 🎵 :
Solving the differential equation xy'+2y=x^3
Solve differential equation xy'+2y= -x^3+x, \ y(1)=2 | Plainmath
Calculus 2 | Solve the Differential Equation xy^2y'=x+10
Differential Equation Variation of Parameters: x^2y'' + xy' - y = x^3 e^x
First Order Linear Differential Equation: xy' + 2y = 4x^2 , y(1) = 2
Differential Equation Variation of Parameters: x^2y'' - 2xy' + 2y = x^3 sin x
Solve: dy/dx + x sin 2y=x^3 cos^2 y || First order ODE || Differential equation
dy/dx=(xy+2y-x-2)/(xy-3y+x-3);Ecuación Diferencial Var.Sep. con separación alternativa de integrales...
How to determine the general solution to a differential equation
solve dy/dx=x³+y³/x²y+xy² ||Homogeneous||Separable||Differential equation
Solve xy^2dy-(x^3+y^3)dx=0 #HomogeneousDifferentialEquation #DifferentialCalculus L389
Differential Equations Practice # 38: (2x^3 - xy^2 - 2y + 3)dx - (x^2y + 2x)dy = 0
Solve: dy/dx = x+2y-3/2x+y-3 | Reducible to homogeneous differential equations
Solve xy'+2y=x+2, Domains of Validity
How to solve dy(x^2y^3 +xy)=dx | Bernoulli's Equation
Solve the differential equation (x-y)dy/dx=x+2y
#13 Non Homogeneous differential Equation 1st order and 1st degree | solve dy/dx=(x-y+3)=(2x-2y+5)
xy' - 2y = x^2
Solve: dy/dx= x^3y^3 -xy || Example of Bernoulli's equation || Step-by-step solution|| 1st orde...
Q137 Solve dy/dx + (x-y-2)/(x-2y-3) = 0
Differential Equation Method of Frobenius: 2xy'' - y' + 2y = 0
Differential Equation Variation of Parameters: x^2y'' + xy' +(x^2 - 1/4)y = x^(3/2)
Show that y = Cx^2 is a solution to the differential equation x*dy/dx = 2y
Solve the linear differential equation xy' = 2y + x^2 【CHILL LO FI VERSION】...
Комментарии
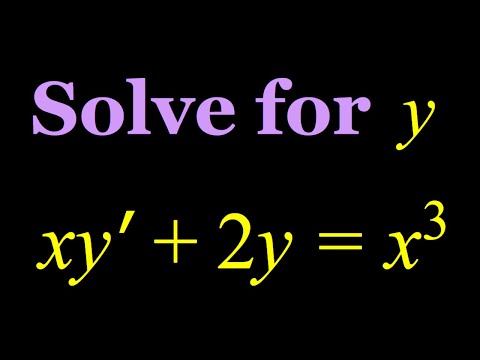 0:08:16
0:08:16
 0:03:25
0:03:25
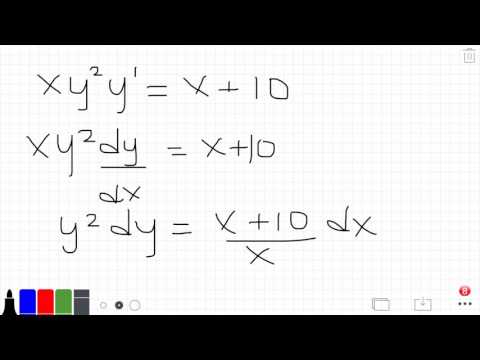 0:02:19
0:02:19
 0:11:41
0:11:41
 0:03:21
0:03:21
 0:07:38
0:07:38
 0:04:37
0:04:37
 0:10:39
0:10:39
 0:02:03
0:02:03
 0:08:28
0:08:28
 0:12:39
0:12:39
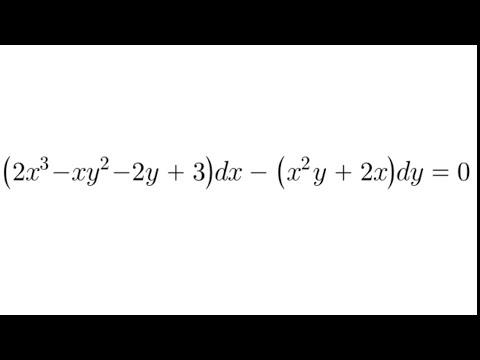 0:05:26
0:05:26
 0:19:17
0:19:17
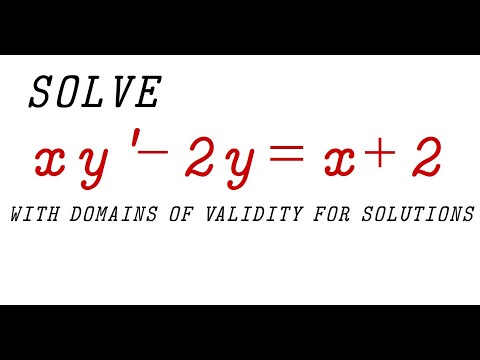 0:05:39
0:05:39
 0:09:35
0:09:35
 0:13:55
0:13:55
 0:22:59
0:22:59
 0:02:03
0:02:03
 0:05:32
0:05:32
 0:22:33
0:22:33
 0:16:08
0:16:08
 0:07:13
0:07:13
 0:01:38
0:01:38
 0:03:00
0:03:00