Calculus 2: Integration (3 of 9) Definite Integral (What is the Integral of Acceleration?)

preview_player
Показать описание

In this video I will explain what is a definite integral and the meaning of the area under the curve.

Next video in the series can be seen at:
  1. Michel van Biezen
  2. ilectureonline
  3. ilectureonline.com
  4. Mike
  5. Mike van Biezen
  6. van Biezen
Рекомендации по теме
Calculus 2: Integration 0:07:28

Calculus 2: Integration (3 of 9) Definite Integral (What is the Integral of Acceleration?)

ALL of calculus 0:08:10

ALL of calculus 3 in 8 minutes.

Calculus 2 - 0:26:12

Calculus 2 - Basic Integration

ALL OF Calculus 0:06:09

ALL OF Calculus 2 in 5 minutes

Calculus 2 In 0:19:35

Calculus 2 In Less Than 20 Minutes (Complete Overview Of Integral Calculus)

Calculus 2: Integration 0:08:52

Calculus 2: Integration - Trig Substitution (3 of 28) Integral of SQRT(x^2-x^2) Ex. 1

calculating work by 0:09:05

calculating work by using integral, pumping water out of a tank, calculus 2 tutorial

What Integration Technique 0:22:40

What Integration Technique Should I Use? (trig sub, u sub, DI method, partial fractions) calculus 2

Calculus NCEA Level 0:59:40

Calculus NCEA Level 2 in 15 hours | Part 4

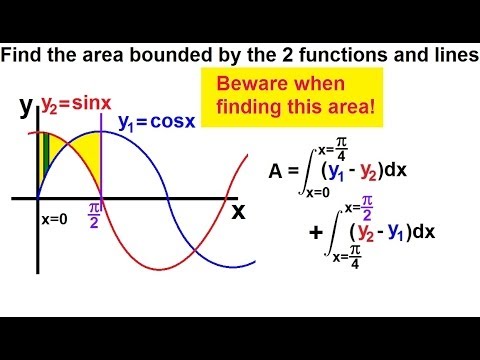
Calculus 2 - 0:08:43

Calculus 2 - Integration: Finding the Area Between Curves (3 of 22) Ex. 3: y=sinx, y=cosx BEWARE!

Integration (Calculus) 0:07:04

Integration (Calculus)

Integral by completing 0:10:13

Integral by completing the square, and u sub, calculus 2

integration by parts, 0:16:59

integration by parts, DI method, VERY EASY

Improper Integrals - 0:13:56

Improper Integrals - Convergence and Divergence - Calculus 2

Calculus 2 Lecture 2:09:24

Calculus 2 Lecture 7.3: Integrals By Trigonometric Substitution

Calculus 2 - 6:52:53

Calculus 2 - Full College Course

Integration and the 0:20:46

Integration and the fundamental theorem of calculus | Chapter 8, Essence of calculus

Triple Integrals - 0:10:06

Triple Integrals - Calculus 3

Calculus 2 Lecture 2:48:31

Calculus 2 Lecture 7.6: Improper Integrals

fast way to 0:05:18

fast way to do partial fraction for integrals, calculus 2 tutorial

How REAL Men 0:00:35

How REAL Men Integrate Functions

Integration By Partial 0:41:07

Integration By Partial Fractions

Calculus 2 Lecture 1:54:37

Calculus 2 Lecture 7.1: Integration By Parts

Calculus in a 0:03:01

Calculus in a nutshell

Комментарии
Автор

Mr. Professor Your lectures ought to be mandatory. It is brilliant.

jakubkusmierczak
Автор

With integral you are not counting velocity, but area!! Derivatives and differences are for the changes over time or locally.

hannukoistinen
Автор

My calculus teacher is horrible at teaching. Thank you for being a great teacher and teaching me Calculus!!

FAWLSSS
Автор

Nice and gentle application of integral.

MrVoayer
Автор

Hi, if the integral of acceleration yields the velocity formula, and we want to find the velocity at t = 5, why we we need the area? Shouldn't we just input t =5 into the velocity formula (which we obtain via integration). Thanks.

MasayoMusic
Автор

How beautiful, thank you for the great explanation! Conceptually, how exactly does the integral work out to be the area underneath the section of the graph? Like why would the velocity be represented by area of the graph?

EP-rqpn
Автор

i think there is a mistake in your solution. 31.25 is the distance not the velocity, because the area below the line is the distance. Also the name of vertical axis is not a but v and its unit is defined by metre per sesond.

kendout
Автор

Can you solve this by using indefinite integral sir?

nellvincervantes