filmov
tv
Proof by Mathematical induction, ∑r^i = (r^(n+1)-1)/(r-1) for r≠0,r ≠1,n∈N. Summation

Показать описание
prove by mathematical induction, summation of r^i from i=0 to n= (r^(n+1)-1)/(r-1) for r≠0,r ≠1,n∈N. calculus.
Proof by Mathematical Induction [IB Math AA HL]
Proof by Mathematical Induction - How to do a Mathematical Induction Proof ( Example 1 )
Algebra 2 – Proof by Mathematical Induction
Proof by Induction : Sum of series ∑r² | ExamSolutions
Mathematical Induction - Proof of ∑r=n(n+1)/2 | ExamSolutions
Prove by induction, Sum of the first n cubes, 1^3+2^3+3^3+...+n^3
Mathematical Induction
A-Level Further Maths: A1-07 Proof by Induction: Sum(1/(r(r+1)))=n/(n+1)
A-Level Further Maths: A1-06 Proof by Induction: Sum(r.r!)=(n+1)!-1
Proof by Mathematical induction, ∑r^i = (r^(n+1)-1)/(r-1) for r≠0,r ≠1,n∈N. Summation
The Binomial Theorem Proof by Induction
A-Level Further Maths: A1-05 Proof by Induction: Sum(r(r+1))=n(n+1)(n+2)/3
Intro to Mathematical Induction
Proof by Induction - Theory & Examples
8.1 Proof by Mathematical Induction (CORE 1- Chapter 8: Proof by induction)
Principle of Mathematical Induction sum(1/(i(i + 1)), i = 1,..., n) = n/(n + 1)
Intro To Math Proofs (Full Course)
Mathematical Induction Made Easy! | IB HL AA and A-Level Further Maths
Proving a Geometric Series Formula with Mathematical Induction
Learn how to use mathematical induction to prove a formula
Mathematical Induction (Harder Inequalities Proof by mathematical induction)
Principle of Mathematical Induction (ab)^n = a^n*b^n Proof
Binomial Theorem || Proof by Mathematical Induction
how to prove by mathematical induction 1(proof by induction)
Комментарии
 0:08:17
0:08:17
 0:07:32
0:07:32
 0:14:33
0:14:33
 0:08:16
0:08:16
 0:08:13
0:08:13
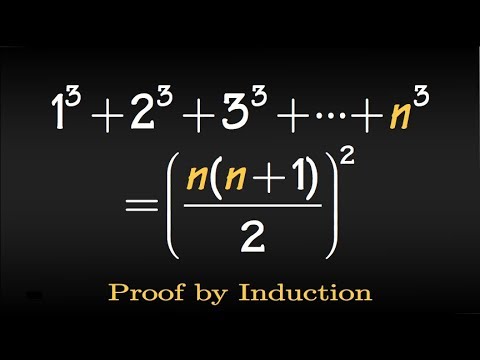 0:09:03
0:09:03
 0:10:04
0:10:04
 0:06:21
0:06:21
 0:08:15
0:08:15
 0:11:42
0:11:42
 0:06:36
0:06:36
 0:04:14
0:04:14
 0:12:15
0:12:15
 0:28:42
0:28:42
 0:32:23
0:32:23
 0:05:48
0:05:48
 2:20:51
2:20:51
 0:32:20
0:32:20
 0:05:53
0:05:53
 0:07:08
0:07:08
 0:13:08
0:13:08
 0:03:52
0:03:52
 0:15:48
0:15:48
 1:23:38
1:23:38