Principle of Mathematical Induction sum(1/(i(i + 1)), i = 1,..., n) = n/(n + 1)

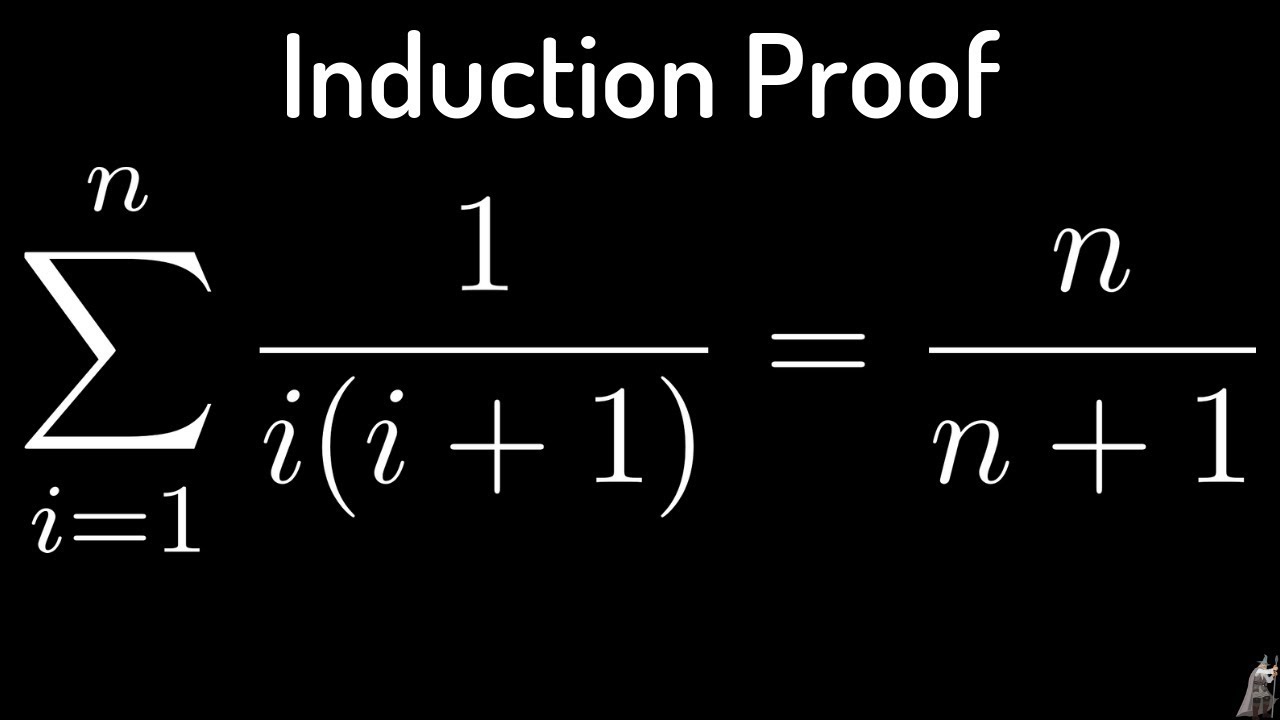
Показать описание

Using the Principle of Mathematical Induction to prove sum(1/(i(i + 1)), i = 1,..., n) = n/(n + 1). I did it for the first time in this video so that maybe it shows you how to figure out problems like this on your own.

Рекомендации по теме

Комментарии

i love how I click on links explaining my late college math and it always links me to the Math Sorc. everytime! you're so helpful. thankyou

michaeltheisen

You have so many videos covering my classes. Ty again as usual. True sorcerer energy.

joshbolton

This video helped me a lot, even in 2020! Thank you so much :)

gracehan

this guy is a legend, still replying to comments

TrymBraathen

That's a great and elegant solution. Thank you, sir!

antoniovianaaa

how did you get k(K+2) +1 on the numerator on the second I.H.?

SnoopyxX

I have a question. If we have n>=0, then will the statement be true. Won't the basis condition change, in that case?

priyanshusharma

What if you start with the top (n) as n+1?

amberanderson

4:25 where do the (k+2) come from? Like how does k become k(k+2)?

flikflak

Thank you so much
Imma subscribe noooow

leilahnabaggala

Can you do one for i x 5^i = 5^n+1 (1/4n - 1/16) + 5/16

dacorgi

gracias loco, abrazote (thanks dude, big hug for u) <3

i'll give u feedback in 12h

jesus_lpz

Great!! Fantastic video! thanks a lot!

gabrielvarela

I want to say! This video helped me 10000% i really didnt know the meaning of "n" but now i do! Im in 7th grade and this helped me!

durondadudley

Principle of Mathematical Induction sum(1/(i(i + 1)), i = 1,..., n) = n/(n + 1)

Mathematical Induction Practice Problems

Proof by Mathematical Induction - How to do a Mathematical Induction Proof ( Example 1 )

Proof by Induction : Sum of series ∑r² | ExamSolutions

Principle of Mathematical Induction sum(1/(i(i + 1)), i = 1,..., n) = n/(n + 1)

Mathematical Induction

Proof by Mathematical Induction | Principle of Mathematical Induction | Sample Problems | Part 1

Prove by the principle of induction for all n belongs to N | 1^2 + 2^2 +...+ n^2 = n(n+1)(2n+1)/6

Proof by Mathematical Induction (Precalculus - College Algebra 73)

Mathematical Induction

Proof by induction | Sequences, series and induction | Precalculus | Khan Academy

Prove by mathematical induction that the sum = n(n+1)/2

Prove by the principle of Mathematical induction |a + ar + ar^2 + …. + ar^(n-1) = a(r^n -1)/(r-1)

Prove by mathematical induction that the sum of squares of positive integers is n(n+1)(2n+1)/6

Prove by Mathematical Induction. Sum = n/n+1

Principle of Mathematical Induction The Sum of the First n Integers Proof

MATHEMATICAL INDUCTION. 1+3+5+7+....+(2n-1)=n^2

Learn how to use mathematical induction to prove a formula

Mathematical Induction Proof with Sum and Factorial

Mathematical Induction Proof for the Sum of Squares

Mathematical Induction Problem 1 - Logic - Discrete Mathematics

Prove by the principle of Mathematical induction | 1^3 + 2^3 + 3^3 + …. + n^3 == [(n(n+1))/2]^2

Prove the following by the principle of induction | 1^2 + 3^2 + 5^2 +…..+ (2n-1)^2 = n(2n-1)(2n+1)/3...

Principle Of Mathematical Induction | Sum Of First n Natural Numbers Using Mathematical Induction

Prove by the principle of Mathematical induction |1/1.2 + 1/2.3 + 1/3.4 + …… + 1/(n(n+1)) = n/(n+1)...