filmov
tv
Can You Solve 4x^3-3x-2=0 in Two Ways?
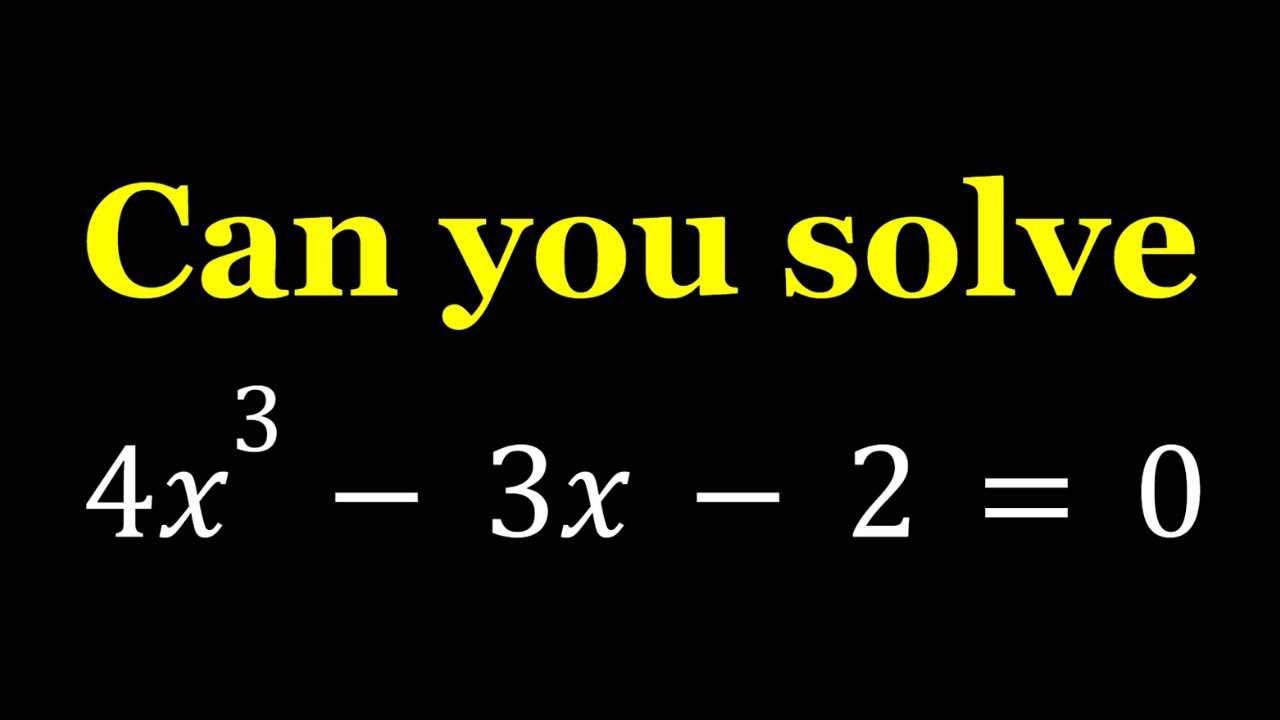
Показать описание
If you need to post a picture of your solution or idea:
#ChallengingMathProblems #PolynomialEquations
⭐ Similar videos:
PLAYLISTS 🎵 :
#ChallengingMathProblems #PolynomialEquations
⭐ Similar videos:
PLAYLISTS 🎵 :
Can You Solve 4x^3-3x-2=0 in Two Ways?
4x^4 - 8x^3 -3x^2 +5x +2 = 0 Steps to Solve Quartic Polynomial Equation
(3x^2+4x-3)-(4x^2-3x+2)=0 | Find The Discriminant & Roots
Example of Quadratic Formula 4x^2+3x-2=0, 4x2+3x-2=0
x^3 - 3x^2 + 4x - 12 factor completely.
Factoring a polynomial to the fourth power using factoring to second power
XQUADOQ002 _ The roots of the equation 3x2 – 4x + 3 = 0 are
x^3 - 4x^2 - x + 4 = 0 solve for x
How to Solve Logarithmic Equations 4 Strategies Advanced Functions
Factor 3x^3 + 4x^2 + x
Factor: x^4 + x^3 - 4x^2 + x +1 | Olympiad Question
Solving an equation with variables on both side and one solution
Factor and Solve Cubic Equations in Less Than One Minute! - Super Simple Trick
Factorising cubic functions: The kx method
Solving a quadratic by completing the square
Solve by Completing the Square: Step-by-Step Technique
3x^2+4x-3=0 . Ecuaciones cuadraticas 3x2+4x-3=0 aplicando formula general , x al cuadrado
How To Factor Polynomials The Easy Way!
3x^2+4x-2=0 . Ecuaciones cuadraticas 3x2+4x-2=0 aplicando formula general , x al cuadrado
Quadratic Equation Solving 3x^2 - 4x + 1 = 0 Step-by-Step | Math Olympiad Question
How to solve 4x^2-3x-2=0 using the Quadratic Formula
Strategies to Solve Multi Step Linear Equations with Fractions
How To Find the Zeros of The Function
Quadratic Equations | Solve by factoring | Free Math Videos
Комментарии
 0:12:19
0:12:19
 0:11:52
0:11:52
 0:03:01
0:03:01
 0:04:23
0:04:23
 0:00:31
0:00:31
 0:03:26
0:03:26
 0:00:40
0:00:40
 0:01:00
0:01:00
 0:05:38
0:05:38
 0:00:54
0:00:54
 0:09:34
0:09:34
 0:02:36
0:02:36
 0:07:18
0:07:18
 0:10:22
0:10:22
 0:10:43
0:10:43
 0:07:40
0:07:40
 0:03:13
0:03:13
 0:11:54
0:11:54
 0:02:55
0:02:55
 0:01:13
0:01:13
 0:02:59
0:02:59
 0:15:41
0:15:41
 0:05:48
0:05:48
 0:02:43
0:02:43