Geometric Algebra - 3D Rotations and Rotors

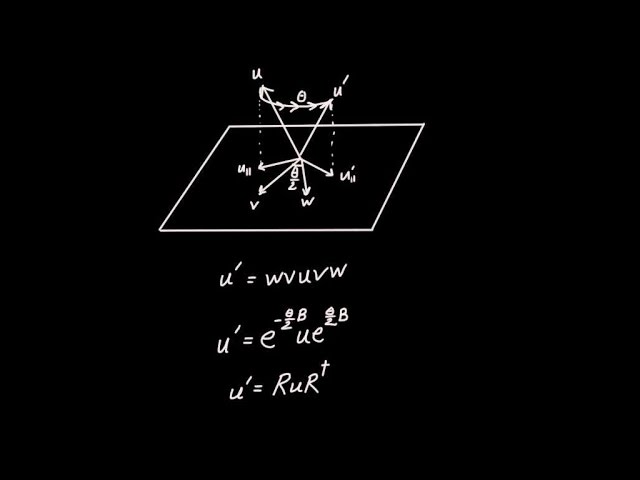
In this video, we employ the fact that two reflections is a rotation to perform rotations in 3D. We also will derive the general rotation formula, show how to compose rotations, and introduce the rotor version of this formula and discover the rotor's sign flip under a 2pi rotation.

References / Further Reading:
1. Lasenby and Doran's "Geometric Algebra for Physicists".

Note: This video builds off prior videos in this series, particularly:

Erratum:
33:50 - the sine function is odd, not even.

[jeanhealey]

WOW! I really enjoy all of these videos. I'm not significantly educated in mathematics and the idea of something that needs to do a 4pi rotation to return to its initial state is something that completely blows my mind and I commend the creator of these videos for simplifying these complex ideas into something that a lay-person like me can play around with and (sort of) understand. AMAZING STUFF!

[albat]

@Matoma, I can't thank you enough for your insightful videos on geometric algebra. This approach is very intuitive and saves a lot of time.

[danielkuntz]

These videos are brilliant! Thank you so much for putting them together. As an engineer who has used complex number and rotation matricies for a ton of stuff, I really appreciate this new conceptual understanding that geometric algebra gives me of them! You make it very easy to understand! I have binge watched all these videos up to this point in utter fascination and don't plan on stopping. Good work!

[kevinportillo]

I had so much trouble understanding why rotations are often in that from. This is so simple to follow an understand. Thank you!

[annakinderman]

These videos are immensely helpful! We are using Geometric Algebra in our Quantum Mechanics class, and there aren't many resources out there for this topic...

[chimetimepaprika]

This is one of my favorite channels ever.

[sdmartens]

Your content is among the best on youtube. I feel like i didn't get a good intuition of what rotors are when not paired with their counterparts. You mentioned there were two ways to perform any rotation theta, is the second way rotating the other way two pi minus theta? Thanks for your time!

[Vannishn]

Hello ! I love your videos, watched the geometric algebra playlist up to here and I have a question. Why couldn't we rotate the projection of a 3d vector u onto the plane of rotation with |u//| exp(theta B) and then add the previously rejected part instead of using the rotor sandwich ?

[jamesmarlar]

I hope you continue this series all the way through Geometric Calculus.

[thomaskaldahl]

48:53
I'm angry I didn't learn about your awesome channel sooner >:(

[jamesking]

Thank you for creating these videos! I was able to implement rotors in my engine after watching them.

[Kelikabeshvill]

You’re awesome! Please do 4 and higher dimension rotations. It would be great to see how those bivectors that are not 2-blades look like

[byronwatkins]

We can always define rotations in higher dimensions similarly, but the physical significance might be less apparent. The exponents are bivectors in the plane of rotation with magnitude angle/2. How that bivector gets constructed is irrelevant, but given two vectors in the plane, angle/2 (u^v)/|u^v| is such a bivector. Given a vector perpendicular to the plane, angle/2 v I /|v| is such a bivector. In a way the tendency of bivectors to rotate is activated by exponentiating it; however, the reflection through the plane that accompanies it must be reversed afterward.

[orsobianco]

I just discovered this very interesting series of videos,
and I thank you a lot for this new (to me) presentation.

I have a small question. Wouldn't it be better to avoid the exponential
notation e^B.theta for cos(theta)+B.sin(theta)?
The exponential notation is usually reserved for commutative algebra
and there is no commutativity here in Clifford algebra.

This notation can be misleading, since
e^B1.theta1 * e^B2.theta2 will generally not be equal to
e^(B1*theta1+B2*theta2) .

As a simple example, consider exp(Pi/2*e1e2) which is e1e2.
If exp(Pi/2*e1e2) * exp(Pi/2*e2e3) = exp(Pi/2*(e1e2+e2e3),
we have e1e2e2e3 = e1e2 + e2e3, thus e1e3-e1e2-e2e3 = 0,
which is impossible as e1e2, e2e3, e3e1 are bivector base elements.

Could you please give me your opinion?
Thank you.

[invid]

Relating to rotating around an axis only working in 2 or 3 dimensions and rotating in a plane generalizing to higher dimensions:
I (used to) like to think of it as rotations in dimension n happening around an object of dimension n - 1
In 2D you rotate around a point, in 3D you rotate around a line, in 4D you would rotate around a plane (as mind-bending as that is)
I have to agree this way of thinking about is much more intuitive

[darthmoomoo]

Are rotations of a vector always in a 2D plane regardless of how many dimensions a space has?

[dsusoftwarecommunity]

Awesome videos! It really helped for me to understand underlying details of 3D rotations! Thanks.

[allanrocha]

Awesome well explained videos! thanks and keep it up!

[KieranORourke]

Bravo! Wonderful series of videos. I was reared on the concept of an 'imaginary scalar' (two words; one fanciful, the other incorrect), justified by some some annoying Polynomialist insisting on a solution to the almost trivial equation x^2+1=0

The fact that this <hack> produced such extraordinary mathematical richness was, for me, an itch I could not scratch, for decades.

Geometric Algebra shivers my tiny brain in it's ability to explain, simplify & clarify the structures I use in Physics and Mathematics, and Quantum Mechanics is being re-written in this language with quiet gasps of "Ah! so that's what I was really doing" .

[alanmochel]

Very well done set of videos introducing geometric algebra along with a single application to Kepler's laws of planetary motion. My only complaint is that it stops at video 13.