filmov
tv
Area & Arc Length of a Cycloid (one arch)
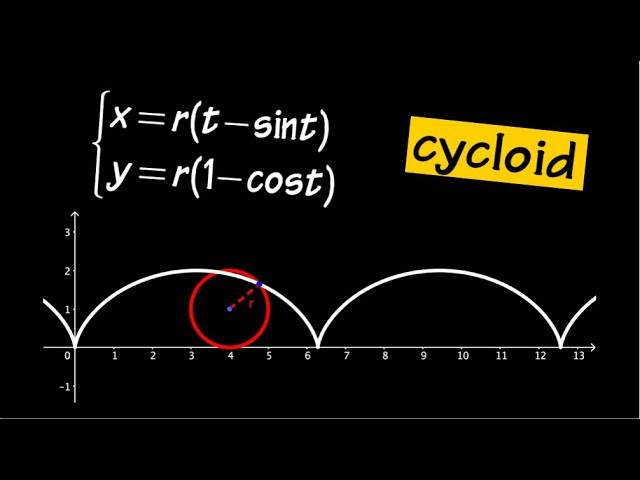
Показать описание
Which one did you like more?
Area of a cycloid, 1:00
Arc Length of a Cycloid, 8:45
Check out my site & social media
Thank you for your support!
blackpenredpen | 曹老師
Arc Length of a Circle Formula - Sector Area, Examples, Radians, In Terms of Pi, Trigonometry
GCSE Maths - Area of a Sector and Length of an Arc of a Circle (Circles Part 3) #108
Arc Length Calculus Problems,
HOW TO FIND ARC LENGTH AND SECTOR AREA OF CIRCLES | GEOMETRY
area and arc length
Arc Length Formula and Sector Area Formula Explained!
Arc Length and Area of a Sector
Arc Length & Surface Area examples
Arc Length (formula explained)
Arc Length and Surface Area
Circles In Geometry, Basic Introduction - Circumference, Area, Arc Length, Inscribed Angles & Ch...
Arc length and sector area [IB Maths AA SL/HL]
Arc length and sector area [IB Maths AI SL/HL]
Length of an Arc, Area of a Sector (Circles) [IB Math AI SL/HL]
Arc Length (Formula)
Area and Arc Length of Circle Sectors
Circular Measure: Arc Length, Sector & Segment Area Formulas
Arc Length and Area of a Sector in a Circle - SAT Math Part 42
Arc Length and Surface Area - Video 1 - Arc Length
Arc Length and Area of a Sector Given Central Angle (Using Proportions)
Circle Sectors - Areas and Arc Lengths | Grade 6+ Series | GCSE Maths Tutor
Arc length intro | Applications of definite integrals | AP Calculus BC | Khan Academy
Partial circle area and arc length
Arc Length & Area of a Sector - Formula & Examples - IGCSE Core & Extended and IB Mathem...
Комментарии
 0:15:57
0:15:57
 0:05:39
0:05:39
 0:30:47
0:30:47
 0:11:32
0:11:32
 0:07:22
0:07:22
 0:05:35
0:05:35
 0:08:43
0:08:43
 0:17:35
0:17:35
 0:07:57
0:07:57
 0:04:06
0:04:06
 0:18:07
0:18:07
 0:09:36
0:09:36
 0:10:18
0:10:18
 0:05:39
0:05:39
 0:01:11
0:01:11
 0:04:56
0:04:56
 0:11:56
0:11:56
 0:06:25
0:06:25
 0:06:25
0:06:25
 0:06:47
0:06:47
 0:20:20
0:20:20
 0:06:21
0:06:21
 0:02:59
0:02:59
 0:19:29
0:19:29