filmov
tv
Linear algebra: 013 Linear transformations I-Definition, Fundamental Theorem, Isomorphism

Показать описание
Linear Algebra 13 : Linear Transformations
Linear transformations and matrices | Chapter 3, Essence of linear algebra
Linear algebra: 013 Linear transformations I-Definition, Fundamental Theorem, Isomorphism
Linear transformations | Matrix transformations | Linear Algebra | Khan Academy
Lecture 13: Matrices and linear transformations
Linear Transformations -- Abstract Linear Algebra 13
Change of basis | Chapter 13, Essence of linear algebra
Linear Algebra - Lecture 19 - The Matrix of a Linear Transformation
2024-Q4-AI 2. Matrix transformations, Linear algebra, OOP
Matrix Transformations and Linear Transformations | Linear Algebra
[Linear Algebra] Linear Transformations
Linear Transformation (Continued): Linear Algebra #13 | ZC OCW
Linear Algebra 19k: Matrix Representation of a Linear Transformation - Vectors in ℝⁿ
Linear Algebra - Lecture 13: Introduction to Linear Transformations
How to Find the Matrix of a Linear Transformation
Linear Algebra 1.8.1 Matrix Transformations
[Linear Algebra] Injective and Surjective Transformations
Finding matrices of compositions of linear transformations
Linear Algebra for Computer Scientists. 13. Transformation Matrices
Linear Algebra - Lecture 16: Composition of Linear Transformations
Matrices for General Linear Transformations | Linear Algebra
KERNEL and RANGE of a LINEAR TRANSFORMATION - LINEAR ALGEBRA
Three-dimensional linear transformations | Chapter 5, Essence of linear algebra
Linear Algebra 15b: What Makes a Transformation Linear?
Комментарии
 0:14:32
0:14:32
 0:10:59
0:10:59
 0:48:54
0:48:54
 0:13:52
0:13:52
 0:45:25
0:45:25
 0:25:07
0:25:07
 0:12:51
0:12:51
 0:10:44
0:10:44
 2:23:10
2:23:10
 0:16:01
0:16:01
![[Linear Algebra] Linear](https://i.ytimg.com/vi/cFIRXQBfgg0/hqdefault.jpg) 0:12:30
0:12:30
 0:40:53
0:40:53
 0:12:40
0:12:40
 0:27:36
0:27:36
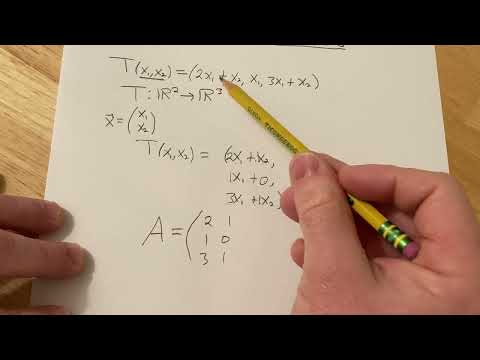 0:05:19
0:05:19
 0:13:49
0:13:49
![[Linear Algebra] Injective](https://i.ytimg.com/vi/WpUv72Y6Dl0/hqdefault.jpg) 0:16:45
0:16:45
 0:08:18
0:08:18
 0:15:44
0:15:44
 0:18:20
0:18:20
 0:18:08
0:18:08
 0:08:46
0:08:46
 0:04:46
0:04:46
 0:08:13
0:08:13