Tangent Planes in Multivariable Calculus

A first look at the tangent plane and normal line, for surfaces defined as z=f(x,y). (Multivariable Calculus Unit 3 Lecture 9)

We define differential functions, derive the tangent plane equation for functions of two variables, and apply this to practical examples. The presentation includes both algebraic and geometric interpretations, emphasizing the importance of partial derivatives and the gradient vector.

Key Points
- Differential functions have well-defined tangent planes.
- The tangent plane equation involves partial derivatives and the gradient vector.
- Understanding tangent planes is crucial in multivariable calculus.
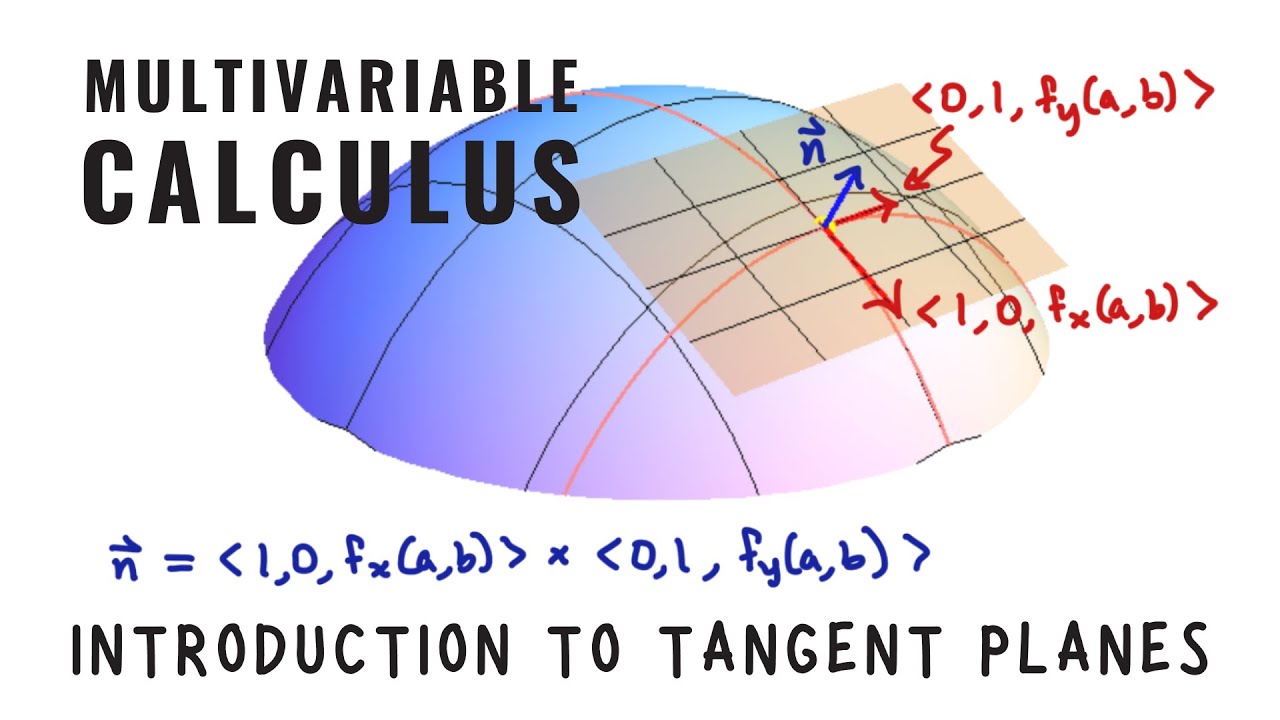
- For a function of the form 𝑧=𝑓(𝑥,𝑦), the tangent plane at (𝑎,𝑏,𝑓(𝑎,𝑏)) is
𝑧=𝑓(𝑎,𝑏)+𝑓𝑥(𝑎,𝑏)(𝑥−𝑎)+𝑓𝑦(𝑎,𝑏)(𝑦−𝑏),
or more concisely,
𝑧=𝑓(𝑎,𝑏)+∇𝑓(𝑎,𝑏)⋅⟨𝑥−𝑎,𝑦−𝑏⟩.
This approach is what I call "Method 1." We will see "Method 2" later.

#calculus #multivariablecalculus #mathematics #tangent #iitjammathematics #calculus3

[yanchaoli]

ex6 at the end of the video, the right side of the 2nd function should be 9 instead of 1 right?

[GG-fd]

Great lecture, very intuitive derivation of the equation of the tangent plane.