filmov
tv
find quadratic equation with a root double the other

Показать описание
certainly! let's go through how to find a quadratic equation where one root is double the other root. we'll derive the equation step-by-step and provide a code example in python.
### understanding quadratic equations
a quadratic equation is generally expressed in the form:
\[ ax^2 + bx + c = 0 \]
where:
- \( a \), \( b \), and \( c \) are coefficients.
- the roots of the equation can be found using the quadratic formula:
\[ x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} \]
### problem statement
let’s say we have two roots: \( r_1 \) and \( r_2 \), where \( r_2 = 2r_1 \).
### step 1: define the roots
let’s denote:
- \( r_1 = r \)
- \( r_2 = 2r \)
### step 2: relationship between roots and coefficients
from vieta's formulas:
1. sum of roots: \( r_1 + r_2 = -\frac{b}{a} \)
2. product of roots: \( r_1 \cdot r_2 = \frac{c}{a} \)
substituting our roots:
1. \( r + 2r = -\frac{b}{a} \) → \( 3r = -\frac{b}{a} \)
2. \( r \cdot 2r = \frac{c}{a} \) → \( 2r^2 = \frac{c}{a} \)
### step 3: choosing coefficient \( a \)
for simplicity, let’s choose \( a = 1 \). thus:
- \( b = -3r \)
- \( c = 2r^2 \)
### step 4: form the quadratic equation
the quadratic equation becomes:
\[ x^2 - 3rx + 2r^2 = 0 \]
### step 5: implementation in code
now, let's implement this in python. we will create a function that takes a root \( r \) and returns the coefficients of the quadratic equation.
### step 6: example calculation
if we take \( r_1 = 2 \), then:
- \( r_2 = 2 \cdot 2 = 4 \)
- the coefficients will be:
- \( a = 1 \)
- \( b = -3 \cdot 2 = -6 \)
- \( c = 2 \cdot 2^2 = 8 \)
thus, the equation will be:
\[ 1x^2 - 6x + 8 = 0 \]
### conclusion
this tutorial has shown how to derive a quadratic equation given that one root is double the other, and provided a simple python implementation to compute the coefficients of the equation. you can modify the root value and see how the equation changes accordingly!
...
#python double or single quotes
#python double array
#python double asterisk
#python double divide
#python double list comprehension
python double or single quotes
python double array
python double asterisk
python double divide
python double list comprehension
python double for loop
python double
python double colon
python double slash
python double underscore
python equation editor
python equation parser
python equation generator
python equation symbols
python equation of state
python equation solve
python equation solver
python equation to latex
### understanding quadratic equations
a quadratic equation is generally expressed in the form:
\[ ax^2 + bx + c = 0 \]
where:
- \( a \), \( b \), and \( c \) are coefficients.
- the roots of the equation can be found using the quadratic formula:
\[ x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} \]
### problem statement
let’s say we have two roots: \( r_1 \) and \( r_2 \), where \( r_2 = 2r_1 \).
### step 1: define the roots
let’s denote:
- \( r_1 = r \)
- \( r_2 = 2r \)
### step 2: relationship between roots and coefficients
from vieta's formulas:
1. sum of roots: \( r_1 + r_2 = -\frac{b}{a} \)
2. product of roots: \( r_1 \cdot r_2 = \frac{c}{a} \)
substituting our roots:
1. \( r + 2r = -\frac{b}{a} \) → \( 3r = -\frac{b}{a} \)
2. \( r \cdot 2r = \frac{c}{a} \) → \( 2r^2 = \frac{c}{a} \)
### step 3: choosing coefficient \( a \)
for simplicity, let’s choose \( a = 1 \). thus:
- \( b = -3r \)
- \( c = 2r^2 \)
### step 4: form the quadratic equation
the quadratic equation becomes:
\[ x^2 - 3rx + 2r^2 = 0 \]
### step 5: implementation in code
now, let's implement this in python. we will create a function that takes a root \( r \) and returns the coefficients of the quadratic equation.
### step 6: example calculation
if we take \( r_1 = 2 \), then:
- \( r_2 = 2 \cdot 2 = 4 \)
- the coefficients will be:
- \( a = 1 \)
- \( b = -3 \cdot 2 = -6 \)
- \( c = 2 \cdot 2^2 = 8 \)
thus, the equation will be:
\[ 1x^2 - 6x + 8 = 0 \]
### conclusion
this tutorial has shown how to derive a quadratic equation given that one root is double the other, and provided a simple python implementation to compute the coefficients of the equation. you can modify the root value and see how the equation changes accordingly!
...
#python double or single quotes
#python double array
#python double asterisk
#python double divide
#python double list comprehension
python double or single quotes
python double array
python double asterisk
python double divide
python double list comprehension
python double for loop
python double
python double colon
python double slash
python double underscore
python equation editor
python equation parser
python equation generator
python equation symbols
python equation of state
python equation solve
python equation solver
python equation to latex
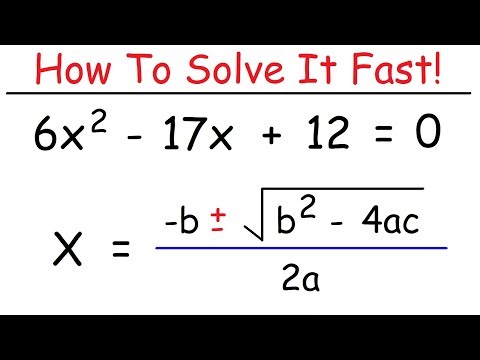 0:05:56
0:05:56
 0:09:35
0:09:35
 0:12:29
0:12:29
 0:01:00
0:01:00
 0:02:43
0:02:43
 0:08:43
0:08:43
 0:13:28
0:13:28
 0:09:05
0:09:05
 0:01:01
0:01:01
 0:03:58
0:03:58
 0:05:17
0:05:17
 0:00:23
0:00:23
 0:07:57
0:07:57
 0:00:54
0:00:54
 0:00:19
0:00:19
 0:13:32
0:13:32
 0:10:16
0:10:16
 0:05:27
0:05:27
 0:00:21
0:00:21
 0:02:46
0:02:46
 0:09:26
0:09:26
 0:00:11
0:00:11
 0:00:53
0:00:53
 0:00:56
0:00:56