filmov
tv
area circle | geometry booster | math olympiad | geometry problems | Masterclass Geometry

Показать описание
Welcome to Masterclass Geometry !!!
Geometry problems from all over the world.
math olympiad geometry | high school geometry | geometry | geometry problems | high school geometry problems | geometry olympiad | geometry olympiad preparation | math olympiad | math olympiad problems | math olympiad problems | premath | andy math | math booster | magda liebt mathe | geometry booster | geometry help | math geometry problems | semi circle area | how to calculate area of circle | circle in quarter circle | high school math problems | right triangle area | pythagorean theorem | pythagorean theorem example | semic circle within semi circle | circle within circle | tangent line | tangent line of circle
#geometryproblems #geometry #geometrydash
Geometry problems from all over the world.
math olympiad geometry | high school geometry | geometry | geometry problems | high school geometry problems | geometry olympiad | geometry olympiad preparation | math olympiad | math olympiad problems | math olympiad problems | premath | andy math | math booster | magda liebt mathe | geometry booster | geometry help | math geometry problems | semi circle area | how to calculate area of circle | circle in quarter circle | high school math problems | right triangle area | pythagorean theorem | pythagorean theorem example | semic circle within semi circle | circle within circle | tangent line | tangent line of circle
#geometryproblems #geometry #geometrydash
area circle | geometry booster | math olympiad | geometry problems | Masterclass Geometry
area circle | geometry booster | math olympiad | geometry problems | Masterclass Geometry
area circle | geometry booster | math olympiad | geometry problems | Masterclass Geometry
A Nice Math Olympiad Geometry Challenge | Circle inside a semicircle | Find the radius of the circle
Find the area of the circle | A Nice Geometry Problem | 2 Different Methods
area semicircle | geometry booster | math olympiad | geometry problems | Masterclass Geometry
area semicircle | geometry booster | math olympiad | geometry problems | Masterclass Geometry
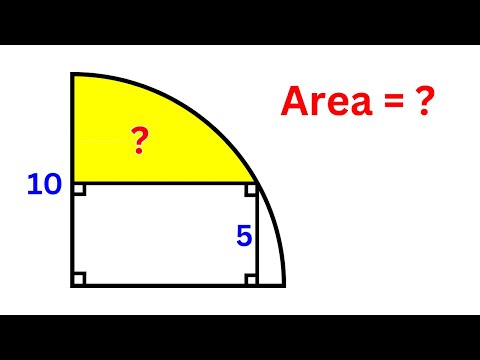
area quarter circle | geometry booster | math olympiad | geometry problems | Masterclass Geometry
area circle in triangle | geometry booster | math olympiad | problems | Masterclass Geometry
area quarter circle | geometry booster | math olympiad | geometry problems | Masterclass Geometry
area semi circle | geometry booster | math olympiad | geometry problems | Masterclass Geometry
area quarter circle | geometry booster | math olympiad | geometry problems | Masterclass Geometry
Russian Math Olympiad | A Very Nice Geometry Problem
area quarter circle | geometry booster | math olympiad | geometry problems | Masterclass Geometry
area circlar ring | geometry booster | math olympiad | area annulus | Masterclass Geometry
Amazing geometric ART hack! Easy circle design✍️😁#shorts #geometricart #drawing #art
Japanese Method #shorts
Very Nice Geometry Problem | Circle and semicircle inside a quarter circle | 2 Methods
A Very Nice Math Olympiad Geometry Problem | Given a circle inside a quarter circle
area circle | square side length | geometry problems | solutions | circle | Masterclass Geometry
Find the blue shaded area | Circle inside a quarter circle | Important Geometry Skills Explained
A Very Nice Geometry Problem | 3 Different Methods
A Nice Geometry Problem | Find the shaded area inside the quarter circle
Japan Math Olympiad | A Very Nice Geometry Challenge
Комментарии
 0:05:03
0:05:03
 0:04:25
0:04:25
 0:03:55
0:03:55
 0:16:01
0:16:01
 0:10:08
0:10:08
 0:04:09
0:04:09
 0:05:07
0:05:07
 0:06:35
0:06:35
 0:06:19
0:06:19
 0:04:05
0:04:05
 0:04:19
0:04:19
 0:03:19
0:03:19
 0:14:34
0:14:34
 0:05:47
0:05:47
 0:03:48
0:03:48
 0:00:27
0:00:27
 0:00:20
0:00:20
 0:16:36
0:16:36
 0:23:58
0:23:58
 0:05:01
0:05:01
 0:05:41
0:05:41
 0:14:14
0:14:14
 0:09:18
0:09:18
 0:10:12
0:10:12