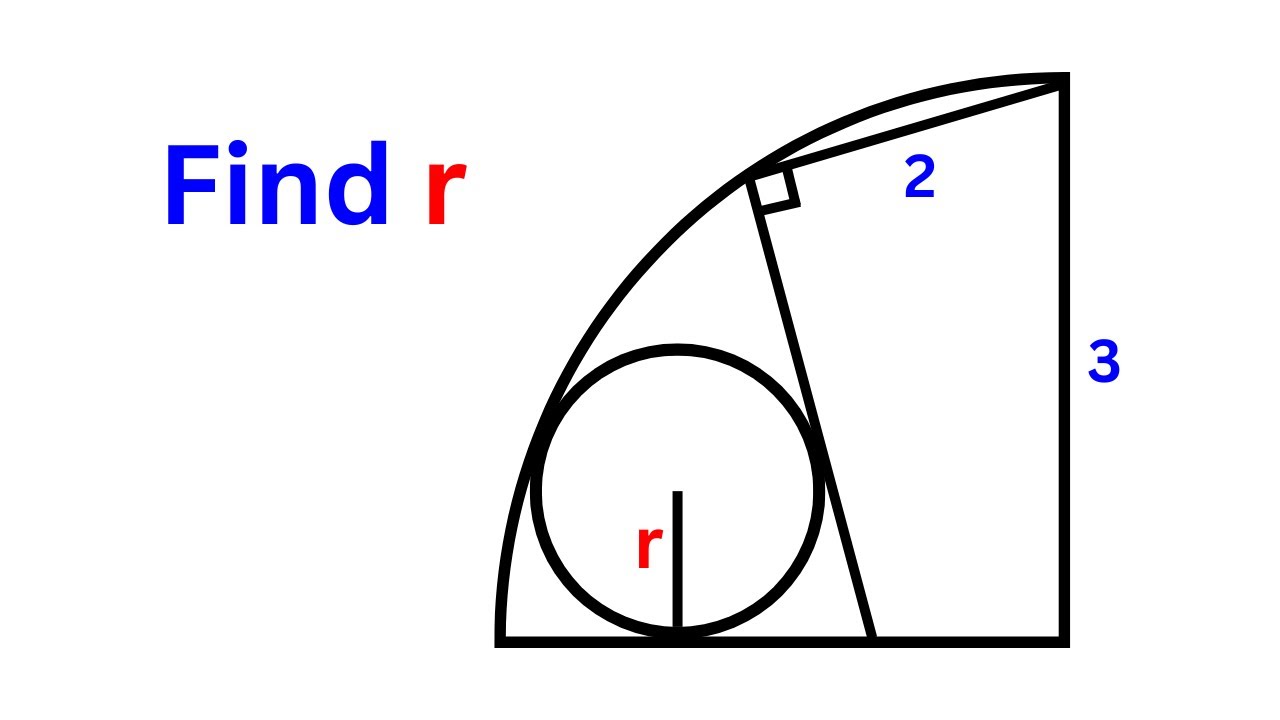
A Very Nice Math Olympiad Geometry Problem | Given a circle inside a quarter circle

A Very Nice Math Olympiad Geometry Problem | Given a circle inside a quarter circle

Join this channel to get access to perks:

MEMBERS OF THIS CHANNEL
••••••••••••••••••••••••••••••••••••••••
Mr. Gnome
ஆத்தங்கரை சண்முகம்
Εκπαιδευτήρια Καντά
AR Knowledge
堤修一
Sidnei Medeiros Vicente
Mark Ludington
Debashis Kesh
Arichai Vattanapat
Sambasivam Sathyamoorthy

[MarieAnne.]

Once we've constructed △CDE (as shown at 5:56) we can find CE using Pythagorean Theorem:
CE = √(DE² − CD²) = √(6² − 2²) = √32 = 4√2
sin 2θ = CE/DE = (4√2)/6 = 2√2/3
cos 2θ = CD/DE = 2/6 = 1/3
tan 2θ = CE/CD = (4√2)/2 = 2√2
We can get tan θ using half-angle identity:
tan θ = (1 − cos 2θ) / sin 2θ = (1 − 1/3) / (2√2/3) = (3−1)/(2√2) = 1/√2

In △OBE
tan2θ = OE/OB → OB = OE/tan2θ = 3/(2√2)
In △ABP
tan θ = AP/AB → AB = AP/tan θ = r/(1/√2) = r√2
In △OAP
AP = r
OA = OB + AB = 3/(2√2) + r√2 = (3+4r)/(2√2)
OP = 3−r
Using Pythagorean theorem, we get:
r² + ((3+4r)/(2√2))² = (3−r)²
r² + (16r²+24r+9)/8 = 9 − 6r+ r²
(16r²+24r+9)/8 = 9 − 6r
16r² + 24r + 9 = 72 − 48r
16r² + 72r − 63 = 0
16r² − 12r + 84r − 63 = 0
4r (4r − 3) + 21 (4r − 3) = 0
(4r + 21) (4r − 3) = 0
Since r > 0, then
*r = 3/4*

[zsboya]

<BCD = <BOD = 90° -> OBCD is a cyclic (inscribed) quadrilateral:
The sides of a chordal quadrilateral are chords of the same circle. The circumferential angle of a chord is constant on the circular arc. ->
<OCB = <ODB, <COD = <CBD, <OBD = <OCD, <CDB = <COB .

[اممدنحمظ]

تمرين جميل جيد . رسم واضح مرتب . شرح واضح مرتب . شكرا جزيلا لكم والله يحفظكم ويرعاكم ويحميكم جميعا . تحياتنا لكم من غزة فلسطين .

[marioalb]

Labelling OB=a, BD=b

sin α = 2/6
α = 19, 4712°

b = 3/ cosα =
b = 3, 18198 cm

Similarity of triangles:
a/b = 2/6
a = 1, 06066 cm

α + 2θ = 90°
θ = 35, 2644°

Tangent secant theorem:
(a + r/tanθ)² = R. (R-2r)
(a + r/tanθ)² = 3(3-2r)
(a + r/tanθ)² = 9-6r

Clearing 'r' :
r = 0.75 cm ( Solved √ )

[quigonkenny]

Extend DO 3 units to E. Extend the arc of the quarter circle around to E to create a semicircle. Extend CB to E. as D and E are ends of a diameter and ∠C = 90, CB is colinear with CE.

Triangle ∆DCE:
DC² + CE² = ED²
2² + CE² = 6²
CE² = 36 - 4 = 32
CE = √32 = 4√2

As ∠EOB = ∠DCE = 90° and ∠BEO = ∠CED, ∆EOB and ∆DCE are similar.

OB/OE = DC/CE
OB/3 = 2/4√2 = 1/2√2
OB = 3/2√2

Let P be the center of the circle, T be the point of tangency between circle P and the circumference of quarter circle O, and V be the point of tangency between circle P and CB. Draw PA, PV, and PB. AB and VB are tangents from circle P intersecting at B, so AB = VB. As PA = PV = r, and PB is shared, ∆PAB and ∆BVP are congruent.

Let ∠ABP = ∠PBV = α. As ∠ABV thus equals 2α, and OA and VE are straight lines, ∠OBE = 2α as well, being a vertical angle of ∠ABV. As ∆EOB and ∆DCE are similar, ∠EDC = ∠OBE = 2α.

tan(2α) = CE/DC = 4√2/2 = 2√2
sin(2α) = CE/ED = 4√2/6 = 2√2/3
cos(2α) = DC/ED = 2/6 = 1/3

tan(2α/2) = sin(2α)/(1+cos(2α))
tan(α) = (2√2/3)/(1+1/3)
tan(α) = (2√2/3)/(4/3)
tan(α) = 2√2/4 = 1/√2

Triangle ∆PAB:
tan(α) = PA/AB
1/√2 = r/AB
AB = √2r

OA = AB + OB
OA = √2r + 3/2√2
OA = (4r+3)/2√2

Draw radius OT. As the centers of two circles are colinear with their point of tangency, OT passes through P. As PT = r and OT = 3, OP = 3-r.

Triangle ∆PAO:
PA² + OA² = OP²
r² + ((4r+3)/2√2)² = (3-r)²
r² + (16r²+24r+9)/8 = 9 - 6r + r²
16r² + 24r + 9 = 72 - 48r
16r² + 72r - 63 = 0
16r² + 84r - 12r - 63 = 0
4r(4r+21) - 3(4r+21) = 0
(4r+21)(4r-3) = 0
r = -21/4 ❌ (r ≥ 0) | r = 3/4 ✓

[marioalb]

sin α = ½ 2 / 3 = 1/3
This right triangle will be named ODC'
C' is midpoint of CD, and C'D=1

Rotate triangle ODC' about O, until align OD and OP:
sin α = 1/3 = r / (R-r)
3.r = R-r
4r = R
r = R/4 = 3/4 = 0.75 cm (.Solved √ )

[zsboya]

We need to prove that the right triangles CDE and APO are similar. In this case, we can calculate "r" very easily with ratio pairs. But how?
\ a = <CED = 90°- 2t & b = <APO = <POD & c = <AOP = 90°- b \
DE/CD = 2R/2 = (R - r)/r -> 3r = 3 - r -> r = 3/4 units.

[marioalb]

Being 'α' the angle between OD and CB, and also between OD and BD, this means α = Angle BDO
sin α = 2 / 6 = 1/3

Also α is angle POA, due to
triangle BDO is similar to triangle POA
r / (R-r) = 1/3
3r = R-r
4r = R
r = ¼R = 3/4 = 0.75 cm ( Solved √ )

[ציוןעמרני-ספ]

In the solution, you assumed that O, P, M reside on the SAME line OM. That enables you to conclude that OP=3-r
How can you prove that?

[tunneloflight]

Btw - your solution is excellent. You may be able to shorten it a bit by bisecting OC (C’ as others suggest), then finding the angle CDO (2 theta) by solving the triangle C’DO, as OC’D must be a right angle. Cos(2 theta) = 1/3 or OC’ = root(9-1) = 2*root(2), so tan(2 theta) = 2*root(2).

[EnnioPiovesan]

As usual I want to try to avoid trigonometry. We assume and accept the fact that: BO=(3/4)√2, CE=4√2, CDE=2ϑ, ABP=ϑ. Now draw from O the perpendicular to the chord CE, which intersects CE itself at R and the (big) circumference at H. We observe that ORE is similar to DCE with a similarity ratio of 1:2, so that RO=(1/2)CD=1.
Consequently HR=HO-RO = 3-1=2. Since the perpendicular to the chord through the center divides the chord itself into two equal parts, CR=RE and therefore RE=(1/2)CE)=2√2. Applying the Pythagorean theorem to the triangle HRE we have: the Pythagorean theorem again to the triangle DHE we have: HD=√(DE²-HE²)= √(36-12)=2√2√3. The ratio HE:HD is therefore 2√3:2√3√2= √2/2. We observe that the two arcs HE and HC are equal and therefore subtend equal angles to the circumference, so (in view of the fact that the total arc CE subtends CDE=2ϑ) HDE=HCD=ϑ. Consequently the right triangles DHE and PAB are similar and therefore HE:HD=PA:AB=r/AB=√2/2 for which AB=r√2. Tracing the ray from O passing through P until it meets the greater circumference in M ​​and the smaller in G, we can write OA²=OM OG --> (AB+BO)²=OM OG --> (r√2+ (3/4)√2)² = 3(3-2r) --> ... 16r²+72r-63=0, which finally yields r=3/4.

[User-jrvf]

Not gonna lie, this one I had to solve in a calculator. And it took me about 2 hours (!!!) to properly set up the problem. As usual I only check the solution in the video after I found the answer myself, and it turns out the method by Math booster is similar to what I used, but her method is easier computation-wise.

[spacer]

If you rotate triangle OPA about O so that OP aligns to OD, it's obvious that triangles OPA is similar to triangle FDC. So OP/PA = FD/CD --> (3-r)/r = 6/2 --> 3-r = 3r --> 3 = 4r --> r = 3/4.

[ΓΕΩΡΓΙΟΣΛΕΚΚΑΣ-μμ]

Στο σημείο που θέλετε να δείξετε ότι <CDO = 2θ μια άλλη δικαιολόγηση: <C+<O=90+90=180, άρα το OBCD είναι εγγράψιμο σε κύκλο οπότε η εξωτερική γωνία ΑΒC = απέναντι εσωτερική CDO. Έτσι: <CDO=2θ

[shalinichawla]

Nice pro If any with easy soln please tell thank you sir❤

[rafael]

I think it is not clear semicircle DCE contains semiquarter circle

[اممدنحمظ]

تمرين جميل جيد . رسم واضح مرتب . شرح واضح مرتب . شكرا جزيلا لكم والله يحفظكم ويرعاكم ويحميكم جميعا . تحياتنا لكم من غزة فلسطين .