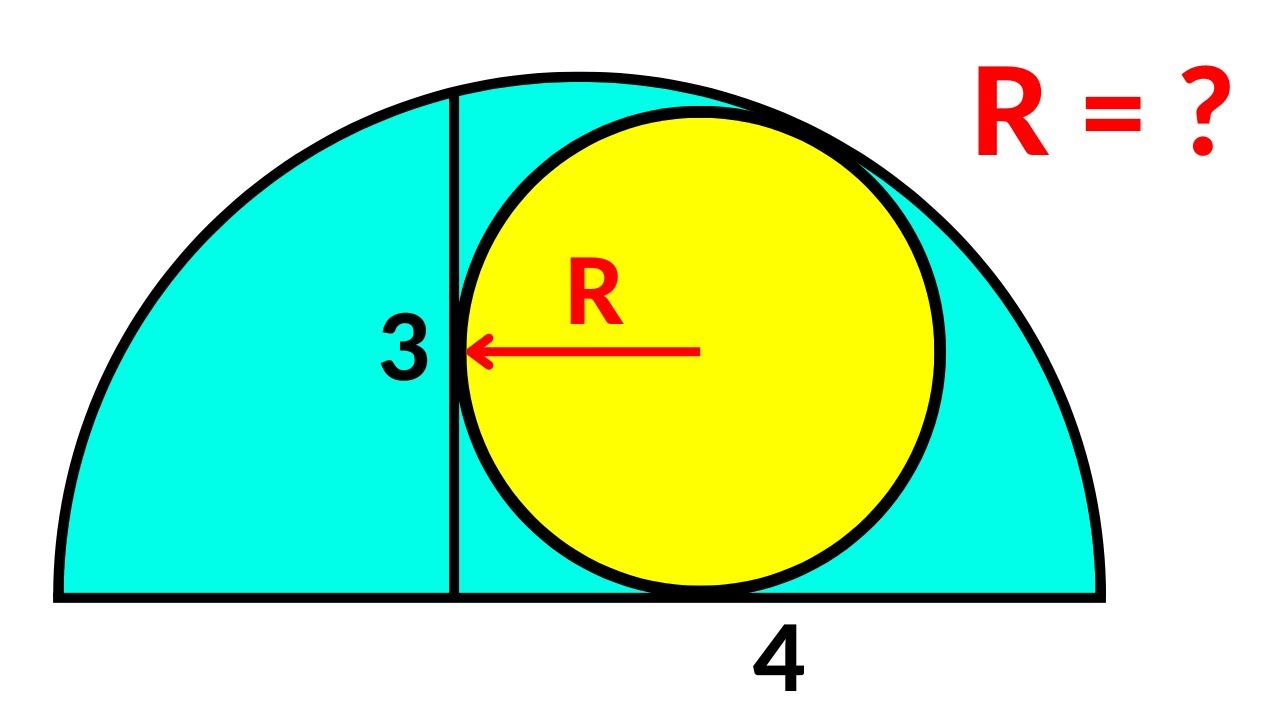
A Nice Math Olympiad Geometry Challenge | Circle inside a semicircle | Find the radius of the circle

A Nice Math Olympiad Geometry Challenge | Circle inside a semicircle | Find the radius of the circle

MY OTHER CHANNELS
••••••••••••••••••••••••••••••••

--------------------------------------------------------------------------------

Become a member of this channel to get access of ULTIMATE MATH COURSE

Join the channel to become a member

[skwest]

Late to the party... but...
1. Complete the circle
2. Extend CD to become a chord.
3. Use Intersecting Chords to establish AD = 9/4.
4. Use #3 to establish point O (center of semicircle) lying on AB, and R (radius of semicircle) as 24/8.
5. Designate point T as the tangent point of the small circle with the semicircle.
6. Connect points O and T to create segment OT, which passes through point o, the center of the small circle (I forget the theorem that makes this so.)
7. Drop a line segment from point o perpendicular to segment OB, intersecting at E, creating right triangle △OEo.
8. The two legs of that right triangle, OE and Eo are (r - 7/8) and r, respectively (where 'r' is the radius of the small circle). The hypotenuse is the semicircle's radius (25/8, see #4) minus r, the small circle's radius.
9. Then, by Pythagoras, we get:
(r - 7/8)² + r² = (25/8 - r)²
10. Simplifying, yields:
r² + (9/2)r - 9 = 0
11. Use the Quadratic Formula to arrive at:
r = 3/2

Ok, now to watch the video and see if I got it right.

[rogeriopessoa]

E se fizessemos: (5-2R)²= (3-R)² + (4-R)², estaria correto? 🤔🤔🤔

[Tmwyl]

Wow! I get every step. The challenge is knowing where to start!!

[mehmetkiraz-wltu]

Bu şekil ve değerler gerçekle uyuşmuyor. Küçük çemberin çapı 3 ise büyük çemberin merkezi; D noktası ile küçük çemberin AB doğrusuna teğet olduğu noktanın tam ortası (O)olmalı. Bu durumda ise büyük çemberin OA ve OB uzunlukları eşit olmuyor.