filmov
tv
Very Nice Geometry Problem | Circle and semicircle inside a quarter circle | 2 Methods
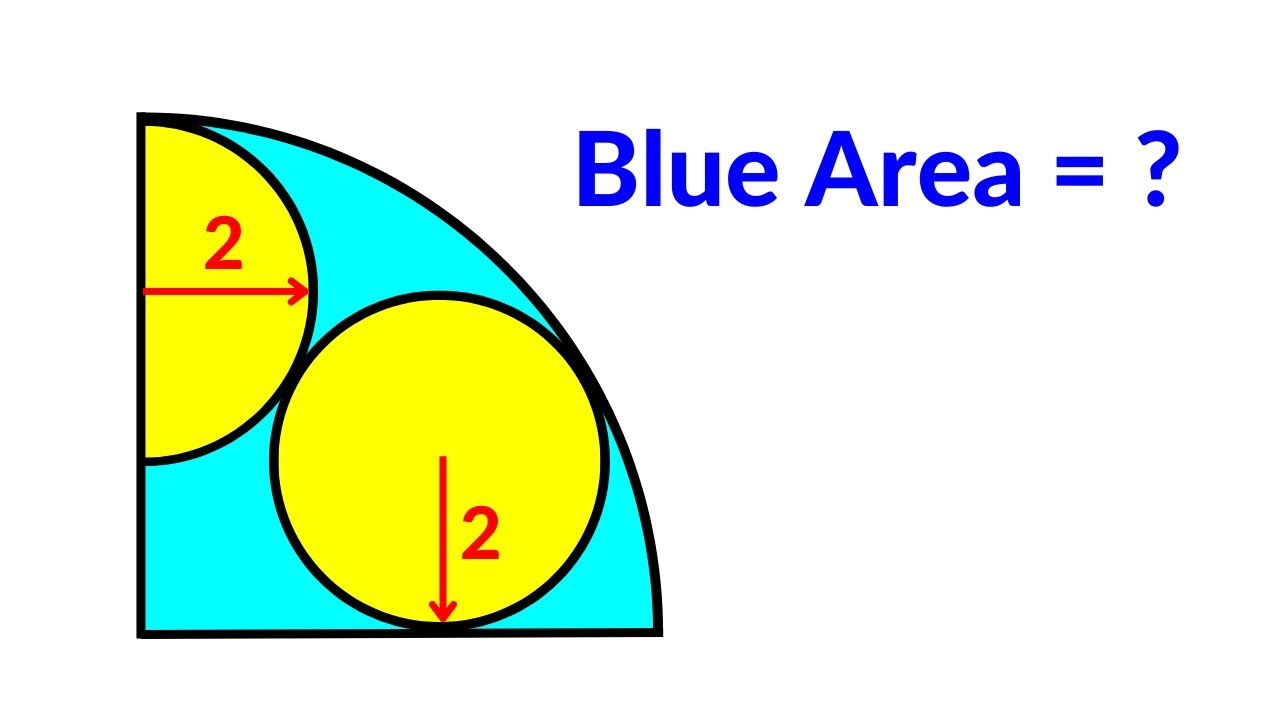
Показать описание
MY OTHER CHANNELS
••••••••••••••••••••••••••••••••
--------------------------------------------------------------------------------
Join the channel to become a member
••••••••••••••••••••••••••••••••
--------------------------------------------------------------------------------
Join the channel to become a member
Can you find the shaded area | A Very Nice Geometry Problem
Very Nice Geometry Problem From Hungary Math Olympiad
A nice geometry problem from New Zealand
Can you find the shaded area in the Rectangle | A Nice Geometry Problem
a nice geometry problem in the complex plane.
Nice geometry problem - area of rectangle?
A relaxing geometry problem.
A nice quick geometry problem.
A Nice Algebra Problem Simplification || Math Olympiad || #maths #education #algebra #mathstricks
End Result Will Shock You!! | Geometry problem
A nice geometry problem with complex numbers.
A nice geometry trick!
A quick geometry problem.
A quick geometry problem.
Clever method to solve a tricky geometry problem!
Missing Angles Geometry Problem | Tricky Math Question | JusticeTheTutor #maths #math #shorts
A viewer suggested geometry problem.
A nice Iranian geometry problem
Fastest Geometry Summary
A beautiful and challenging geometry construction
A Tricky Geometry Problem Solved In 2 Ways!
Evil Geometry Problem
Awesome Problem!
My Geometry Dash Difficulty Faces! (Original)
Комментарии
 0:09:07
0:09:07
 0:18:35
0:18:35
 0:06:36
0:06:36
 0:07:15
0:07:15
 0:09:23
0:09:23
 0:06:39
0:06:39
 0:06:13
0:06:13
 0:04:58
0:04:58
 0:06:58
0:06:58
 0:10:09
0:10:09
 0:11:39
0:11:39
 0:12:30
0:12:30
 0:05:49
0:05:49
 0:08:22
0:08:22
 0:03:15
0:03:15
 0:00:37
0:00:37
 0:10:35
0:10:35
 0:05:34
0:05:34
 0:02:52
0:02:52
 0:04:49
0:04:49
 0:05:02
0:05:02
 0:03:23
0:03:23
 0:01:56
0:01:56
 0:00:22
0:00:22