filmov
tv
Solving A Nice Radical Equation

Показать описание
🤩 Hello everyone, I'm very excited to bring you SyberMath Shorts!
Enjoy...and thank you for your support!!! 🧡🥰🎉🥳🧡
If you need to post a picture of your solution or idea:
#algebra #counting #geometry #numbertheory #calculus
via @YouTube @Apple @Desmos @NotabilityApp @googledocs @canva
PLAYLISTS 🎵 :
Enjoy...and thank you for your support!!! 🧡🥰🎉🥳🧡
If you need to post a picture of your solution or idea:
#algebra #counting #geometry #numbertheory #calculus
via @YouTube @Apple @Desmos @NotabilityApp @googledocs @canva
PLAYLISTS 🎵 :
Solving Radical Equations
A Nice Radical Equation Solved in Three Ways
Solving a nice radical equation
Solving a nice radical equation
A Nice Radical Equation | Easy Solution Method #maths
Solving a Nice Radical Equation in Two Ways
Solving A Nice Radical Equation
Solving A Nice Radical Equation | How To Solve Radical Equation With Two Radicals.
The Easiest Way to Master MATH | Radical Equations
Solving Radical Equations With Square Roots, Cube Roots, Two Radicals, Fractions, Rational Exponents
A Quick and Easy Radical Equation
A Nice Radical Equation with Fifth Root
A Very Nice Math Olympiad Problem | Solve the Radical Equation| Algebra
Solve Radical Equations like a Pro with This Proven TRICK!
Can You Solve a Radical Equation?
Solving radical equations | Exponent expressions and equations | Algebra I | Khan Academy
A Nice Algebraic Radical Problem #shorts #olympiad #maths #mathematics #tips #matholympiad #algebra
Solving A Radical Equation | Algebra
Simplifying A Nice Radical Expression
Solving A Radical Equation #algebra #radicals #radicalequations
Solving A Nice Radical Equation
Solving a Nice Radical System in Two Ways
Solving Radical Equations
Evaluating a Nice Radical Expression in Two Ways
Комментарии
 0:17:11
0:17:11
 0:08:51
0:08:51
 0:09:04
0:09:04
 0:08:21
0:08:21
 0:03:05
0:03:05
 0:11:59
0:11:59
 0:08:53
0:08:53
 0:19:51
0:19:51
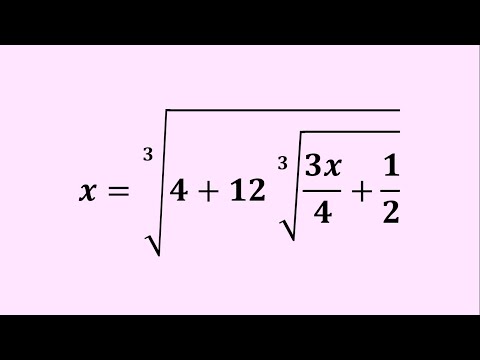 0:12:23
0:12:23
 0:18:05
0:18:05
 0:09:16
0:09:16
 0:08:49
0:08:49
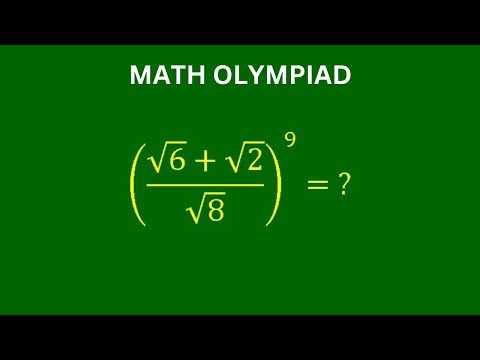 0:20:01
0:20:01
 0:11:57
0:11:57
 0:00:31
0:00:31
 0:03:11
0:03:11
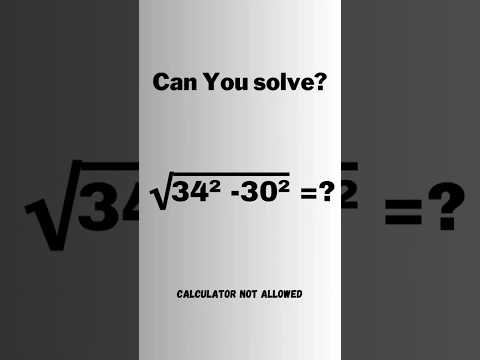 0:00:44
0:00:44
 0:00:29
0:00:29
 0:00:39
0:00:39
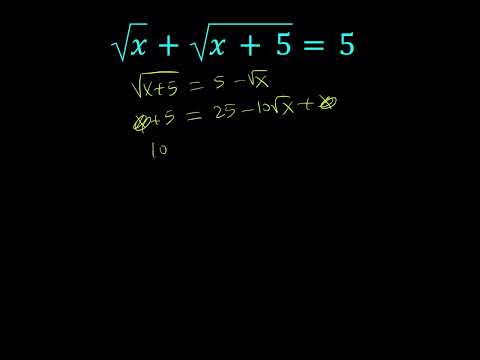 0:00:31
0:00:31
 0:06:51
0:06:51
 0:09:12
0:09:12
 0:03:31
0:03:31
 0:09:35
0:09:35