filmov
tv
Find q so that x^4-40x^2+q=0 has 4 solutions forming an arithmetic progression. German Math Olympiad
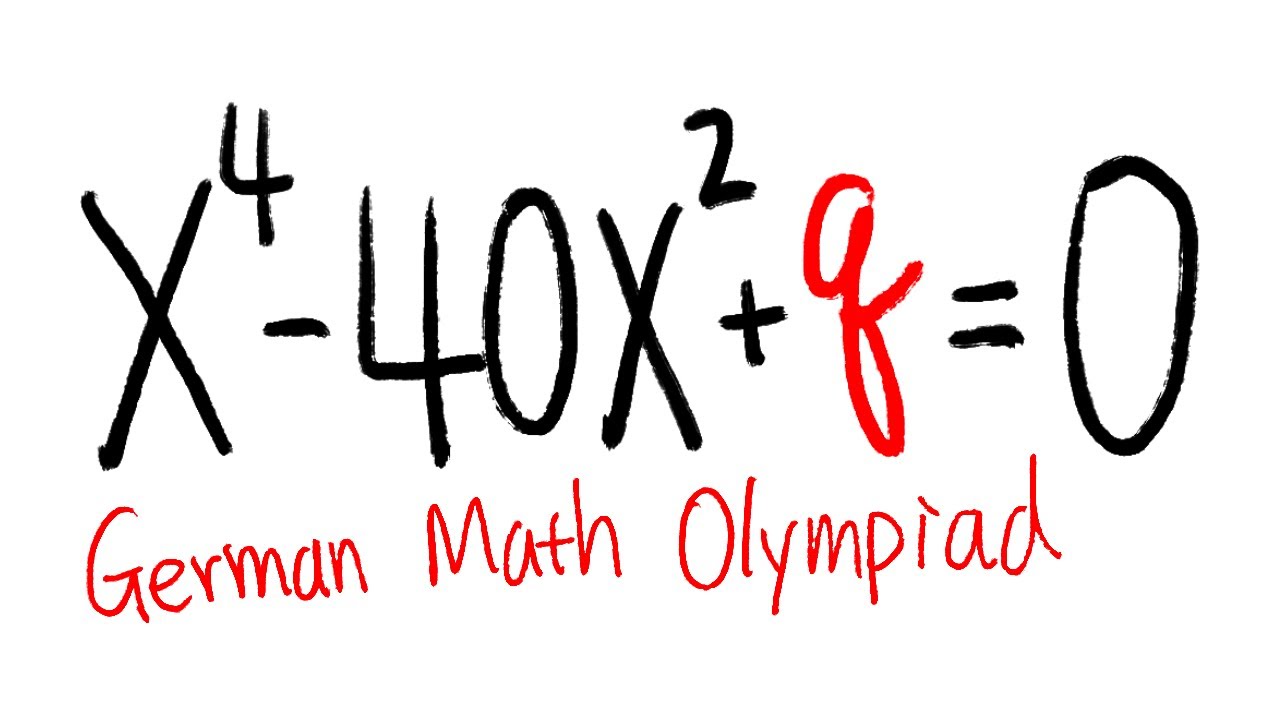
Показать описание
Here's a quartic problem on the German math olympiad. We want to find q so that the equation x^4-40x^2+q=0 has 4 solutions forming an arithmetic progression. Mathematical Olympiad.
----------------------------------------
#blackpenredpen #math #calculus #apcalculus
----------------------------------------
#blackpenredpen #math #calculus #apcalculus
Find q so that x^4-40x^2+q=0 has 4 solutions forming an arithmetic progression. German Math Olympiad
Factoring a polynomial to the fourth power using factoring to second power
Find q such that root(4 real roots) are in A.P
How To Solve Absolute Value Equations, Basic Introduction, Algebra
Synthetic Division of Polynomials
Solve by Completing the Square: Step-by-Step Technique
Solving a quadratic by completing the square
How to solve a 5-term 4th degree polynomial equation x^4+x^3+x^2+x+1=0
Determine Maximum Profit From Revenue and Cost Function
India vs japan || mathematics challenge || 😅🤣🤣🤭
Solve Quadratic Equations By Factoring - Simple Trick No Fuss!
Solving an equation for y and x
how to write a polynomial in the P(x)=Q(x)D(x)+R(x) form
Why are these chords SO beautiful? | Q+A
ASVAB/PiCAT Arithmetic Reasoning Practice Test Q: Ratios/Proportions #acetheasvab with #grammarhero
given demand & cost function find price function total revenue function & profit Maximizing ...
Salsa Night in IIT Bombay #shorts #salsa #dance #iit #iitbombay #motivation #trending #viral #jee
HP Laptop Startup Boot Menu - Quick Guide
Find the value of ‘K’ for which the quadratic equation 2kx^2-40x+25=0 has real and equal roots
Quadratic Equation (WORD PROBLEMS) [First Year (XI) Mathematics] Exercise 4 .10 ( Q # 6,7,8,9,10) 😷...
AAI JE ATC EXAM DEC 2023 Shift 2 Solved paper Maths part 4/Maths topics,formulae & solution for ...
Setup/Pair BMW to Garage Door (2 Ways)
Green Day - When I Come Around [Official Music Video] (4K Upgrade)
Germany Math Olympiad, a system of cubic equations
Комментарии
 0:10:23
0:10:23
 0:03:26
0:03:26
 0:10:00
0:10:00
 0:04:21
0:04:21
 0:10:32
0:10:32
 0:07:40
0:07:40
 0:10:43
0:10:43
 0:13:19
0:13:19
 0:03:49
0:03:49
 0:00:12
0:00:12
 0:06:31
0:06:31
 0:03:47
0:03:47
 0:05:38
0:05:38
 0:13:09
0:13:09
 0:01:00
0:01:00
 0:04:46
0:04:46
 0:00:14
0:00:14
 0:00:23
0:00:23
 0:12:34
0:12:34
 0:26:03
0:26:03
 0:08:45
0:08:45
 0:02:24
0:02:24
 0:03:00
0:03:00
 0:11:36
0:11:36