filmov
tv
Optimization - Open Box With Max Volume | JK Math
Показать описание
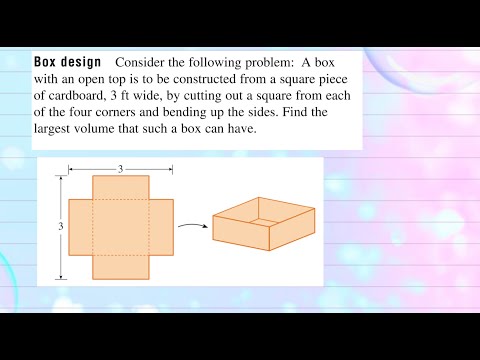
In this video we look at how to solve a specific calculus optimization problem dealing with the maximum volume of an open-top box. Specifically, we look at the following problem: An open-top box is to be constructed from a 14 by 30 cm piece of cardboard. To do this, squares of equal size must be cut from the four corners, so the sides can be bent upwards. What should the dimensions of the squares be to create a box with the largest possible volume?
Video Chapters:
0:00 Problem Reading
0:39 Labeling The Diagrams
3:22 Finding & Simplifying the Volume Equation
5:17 Determining The Domain
7:12 Taking the Derivative & Solving for x
11:19 Outro
More Videos on Optimization:
Playlists:
⚡️Math Products I Recommend⚡️
⚡️Textbooks I Use⚡️
⚡️My Recording Equipment⚡️
(Commissions earned on qualifying purchases)
Find me on social media:
Instagram: @jk_mathematics
Thanks for watching! Any questions? Feedback? Leave a comment!
-Josh from JK Math
#calculus #derivatives
Disclaimer: Please note that some of the links associated with the videos on my channel may generate affiliate commissions on my behalf. As an amazon associate, I earn from qualifying purchases that you may make through such affiliate links.
0:10:33
Maximize Volume of an Open Top Box (Optimization) | Calculus 1 Exercises
0:06:46
Optimization: Minimize Surface Area of a Box Given the Volume
0:11:44
Optimization - Open Box With Max Volume | JK Math
0:08:05
Optimization: Find Largest Volume of a Box Given Amount of Material
![4.5#5: [Part 1]](https://i.ytimg.com/vi/o0kNBWM8Md8/hqdefault.jpg)
0:21:45
4.5#5: [Part 1] Optimization: Open Box problem: idea, animations and set up
0:06:18
Calculus optimization: given surface area, want largest volume of an open-top box
0:05:56
How to Solve an Optimization Problem (Open Box Problem)
![[HD] Optimization -](https://i.ytimg.com/vi/78EedH9ZJRE/hqdefault.jpg)
0:10:17
[HD] Optimization - Open Box & Cost Problem (Pre-Calculus version)
0:05:47
Volume of Open Box Made From Rectangle with Squares Cut Out
0:09:54
Optimization in Calculus | Finding the largest volume possible for an open top box
0:11:12
Optimization Question - Corner Cut to form a Box
0:06:49
Calculus - Optimization - Open Box
0:11:23
Optimization - Minimize Cost Of A Box
0:11:33
4.5B Optimization (Maximize the Volume of an Open Box)
0:12:01
Optimization | minimize surface area | box with square base and open top given volume calculus
0:16:10
Optimization Example (box)
![4.5#5 [Part 2]](https://i.ytimg.com/vi/jdnCH6LappI/hqdefault.jpg)
0:16:36
4.5#5 [Part 2] Optimization: Open Box problem: solving the problem via Calculus
0:08:39
Optimization: Minimized the Surface are of an Open Top Box
0:06:41
Optimization, a box with an open top, given volume, find the minimum surface area
1:02:19
Optimization Problems - Box, Fence, Open Box, Cylinder, Distance - Calculus
0:06:46
Optimization - Minimize Cost given a Specific Volume of an Open Top Box
0:21:03
How to Solve ANY Optimization Problem | Calculus 1
0:11:02
Optimization | folding box | maximize volume of box calculus
0:09:24
Optimisation Using Calculus - Maximizing Volume of an Open Box
Комментарии