Volume of Open Box Made From Rectangle with Squares Cut Out

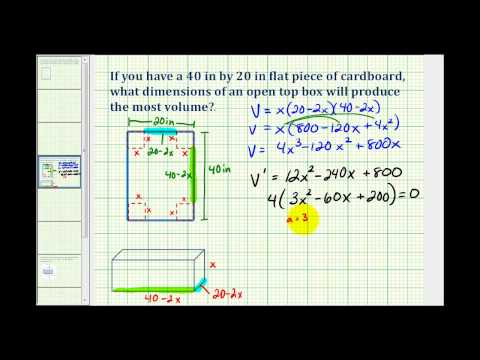
Learn how to find the volume of an open box made from a rectangle with squares cut out of the corners. We discuss the domain restrictions, the graph, and how to maximize the volume in this free math video tutorial by Mario's Math Tutoring.

0:23 Diagram of Rectangle with Squares Removed
1:09 How to Write the Volume of the Box as a Function of x
1:38 Analyzing the Domain of the Function by Writing Inequalities
3:40 Graphing the Inequalities and Identifying the Intersection
3:59 Graphing the Function with Zeros and End Behavior
4:35 How to Find the Maximum Volume on the Restricted Domain
4:49 If You are in Calculus You Can Use the Derivative to find the Max

Looking to raise your math score on the ACT and new SAT?
Check out my Huge ACT Math Video Course and my Huge SAT Math Video Course for sale at

For online 1-to-1 tutoring or more information about me see my website at:

* Organized List of My Video Lessons to Help You Raise Your Scores & Pass Your Class. Videos Arranged by Math Subject as well as by Chapter/Topic. (Bookmark the Link Below)

[davideographer]

Well explained, thank you for being a lifesaver!

[DavidP-vnwp]

You’ve done what my professor could not. Thank you so much!!!!

[Mud-Sock-Girl]

Hi; I am in charge of teaching 11th grade math to my daughter due to Covid-19 homeschooling. So far, I have had better recall of my college Calculus classes in helping her than I thought I would; which was nearly 25 years ago. She is currently finding not only the max val of the open boxes, but also needs to find the dimensions of the cut out box. Since, we don't have a graphing calculator at home, I taught her to take derivatives to find the max values--she gets that just fine. Do you have any videos of find the cut out dimensions? Thanks so much

[deformedalbinogamingcat]

This helped a lot. I sat here looking at my sheet or device (since covid just kinda came) in bewilderment as my teacher never even showed us anything along these lines - or I just forgot. Regardless, you’re a lifesaver.

[jjuan]

Hello, im a grd 12 calculus student and thank you so much for showing me how this worked. I was wondering what the missing sides represented since we dont know, but saying it was x just started churring my brain to max. Thank you for the win

[najeebbagan]

35 seconds in and my problem was solved. bless

[whatsunderthetable]

shout out to you, i never understood this question and it kept popping up in my class, thanks!!

[jess-pnno]

I wouldn’t have passed algebra this semester if it weren’t for you; genuinely, thank you

[hidayatirauhah]

Thanksss!!! But how we know that the height of the box that we built is x?

[gamingtheory]

I don't have to have this in a graph. My homework is asking me to: Write a formula to represent the volume of the box as a function of x. I don't know how to do that though. Do you think you could help me?

[sakshamdhillon]

Excellent work man you save my assignment

[jackiebeng]

Thank you! This helped clarfify my Calc HW!

[jomo]

An open top box is to be made by cutting congruent square form the corners of an 8-inches sheet of tin and then folding up the sides. What should be the dimensions of the box so as to maximize its volume? Can you solve this for pls😢

[sahibmoga]

Thank you Mario! Great explanation of the problem

[ccorpses]

Literally the best… I constantly get stuck as I am in an advanced grade and what’s worse is that it’s even more advanced because it’s honors. You constantly save me… my go-to! Tysm :D

[matttzzz]

This was in my test today. My teacher asked us to find the volume, V, in terms of m and x. Where m is the original side length of the single uncut square and x is the side lengths of each corner squares. He then asked us to state the inverse of V(x). My calculator gave me a ridiculous long equation involving trigs and inverse trigs. He then asked us to find x in terms of m, if the volume is 300 cubic units. The calculator gives an even more ridiculous equation. He then asked for the surface area, S, in terms of m. More ridiculous. Then asked for the derivative function dS/dm. My calculator gave me an equation so long and so convoluted that it would take forever to merely copy it from the calculator to the paper and it seemed like it didnt have an end to it!
He then asked: "show that the tangent of the point (m/8, 0) on V(x) has a positive gradient for all positive values of m.".
This is crazy, because if m=0 then the tangent has a positive gradient and if m>0 then the tangent MUST be zero. Hence the tangent cannot have a positive gradient for positive values of m. If you draw the graph V(x) you'll see its a positive cubic with an intercept at (0, 0) and local minimum turning point at (m/2, 0). Since i found V(x) to be V(x)=x(2x-m)^2.

Edit: ok i just realized i could have substituted x=m/8 into dV/dx to show that dV/dx is (3m^2)/16... which is positive for all values of positive m... its so easy now that I'm home and relaxed. But during the test it felt impossible.

[soldierzoom]

just got this as homework and they just give answer with no explanation so thx for the help

[Абдулазиз-дц]

could you explain why do we indicate the height as x, please

[k_rudy]

really easy to understand thanks for the help

[NikitaNair]

Thank you so much!!! This helped me so much