filmov
tv
Optimization | folding box | maximize volume of box calculus

Показать описание
In this example problem, a piece of cardboard is formed into an open-top box by cutting squares with side length x from each corner and folding up the sides. Find a formula for the volume of the box in terms of x. Then find the value of x that will maximize the volume of the box.
We work an optimization problem by setting up an objective function based on removing the squares in the corners. After expanding the volume function, we take the derivate. Setting the derivative equal to zero and solving down gives two values for x. Only one works based on the dimensions given to us for the cardboard. We then take the second derivative of the volume function and use the second derivative test to check that the function is concave down at our value of x. This ensures that we will have a maximum volume at the value that we found.
We work an optimization problem by setting up an objective function based on removing the squares in the corners. After expanding the volume function, we take the derivate. Setting the derivative equal to zero and solving down gives two values for x. Only one works based on the dimensions given to us for the cardboard. We then take the second derivative of the volume function and use the second derivative test to check that the function is concave down at our value of x. This ensures that we will have a maximum volume at the value that we found.
Optimization Question - Corner Cut to form a Box
Optimization | folding box | maximize volume of box calculus
How to Solve an Optimization Problem (Open Box Problem)
Optimization - Open Box With Max Volume | JK Math
The Box of Maximum Volume Problem - Univariate Optimization
4.5#5: [Part 1] Optimization: Open Box problem: idea, animations and set up
📦 Optimization Problem #5: Maximizing the Volume of a Box from a Square Material 📦
Maximize Volume of an Open Top Box (Optimization) | Calculus 1 Exercises
Optimization Box Problem
Optimization - Box with Cut Corners
Optimization Practice Problem #2: The Cardboard Box Problem
Wk-11 Derivatives: Optimization (Volume) - Open Top Box from Cardboard
Optimization: Maximize Volume of a Box
(Optimization) - Finding the Maximum Volume of a Box
Optimization Example 5 Box
Optimization Video: Optimizing Volume of Boxes
Optimization: Largest volume open top box
Optimization Box Via Tabs
Optimization Problems Involving Boxes and Trays
Dimensions of Box with Largest Volume | Calculus Optimization Problem
From Paper Folding to Open Box: Popular Optimization Question
Optimization Problem: Part2: Minimizing the Cost Function & Open Box Problem
4.5B Optimization (Maximize the Volume of an Open Box)
Optimization Maximize Volume of Box
Комментарии
 0:11:12
0:11:12
 0:11:02
0:11:02
 0:05:56
0:05:56
 0:11:44
0:11:44
 0:12:11
0:12:11
![4.5#5: [Part 1]](https://i.ytimg.com/vi/o0kNBWM8Md8/hqdefault.jpg) 0:21:45
0:21:45
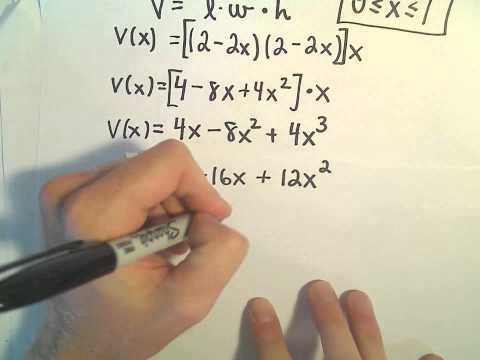 0:10:58
0:10:58
 0:10:33
0:10:33
 0:10:14
0:10:14
 0:09:54
0:09:54
 0:21:26
0:21:26
 0:04:42
0:04:42
 0:09:24
0:09:24
 0:06:51
0:06:51
 0:12:57
0:12:57
 0:18:42
0:18:42
 0:09:21
0:09:21
 0:30:01
0:30:01
 0:09:45
0:09:45
 0:07:35
0:07:35
 0:00:56
0:00:56
 0:47:38
0:47:38
 0:11:33
0:11:33
 0:09:58
0:09:58