filmov
tv
Discrete Math - 5.2.1 The Well-Ordering Principle and Strong Induction

Показать описание
In this video we introduce the well-ordering principle and look and one proof by strong induction.
Video Chapters:
Introduction 0:00
The Well-Ordering Principle 0:10
Postage Stamp Example Using Induction 2:11
Postage Stamp Example Using Strong Induction 7:01
Up Next 9:35
Textbook: Rosen, Discrete Mathematics and Its Applications, 7e
Video Chapters:
Introduction 0:00
The Well-Ordering Principle 0:10
Postage Stamp Example Using Induction 2:11
Postage Stamp Example Using Strong Induction 7:01
Up Next 9:35
Textbook: Rosen, Discrete Mathematics and Its Applications, 7e
Composition of Relation with Itself
Composition of relations | MISTAKE - explained RoS instead of SoR and vice versa | otherwise correct
Discrete Math II - 5.2.1 Proof by Strong Induction
Discrete Math - 5.1.1 Proof Using Mathematical Induction - Summation Formulae
COMBINATIONS with REPETITION - DISCRETE MATHEMATICS
Discrete Math - 5.3.1 Revisiting Recursive Definitions
Discrete Random Variables The Expected Value of X and VarX
Solving congruences, 3 introductory examples
Introduction to Relations
Discrete Math Proofs in 22 Minutes (5 Types, 9 Examples)
Discrete Math 5.3.1 Recursive Definitions
Math Prof answers 6÷2(1+2) = ? once and for all ***Viral Math Problem***
[Discrete Mathematics] Midterm 1 Solutions
Recursive Formulas For Sequences
Warshall's Algorithm (Finding the Transitive Closure)
Recurrence Relations Problem 1 - Recurrence Relation - Discrete Mathematics
[Discrete Mathematics] Midterm 2 Solutions
Discrete Mathematics Lecture 2 | Principle of Mathematical Induction By Dr.Gajendra Purohit
The Hardest Math Test
What is Modular Arithmetic - Introduction to Modular Arithmetic - Cryptography - Lesson 2
Introductory Discrete Mathematics by V.K. Balakrishnan
Equivalence Relation
Discrete mathematics by Dr. Abdur Rehman | chapter 5 Number Theory Exercise 5.2 question 1 |
functions explained in 17 seconds! (Algebra 1)
Комментарии
 0:06:59
0:06:59
 0:03:20
0:03:20
 0:16:22
0:16:22
 0:23:24
0:23:24
 0:13:35
0:13:35
 0:20:39
0:20:39
 0:05:33
0:05:33
 0:03:51
0:03:51
 0:07:39
0:07:39
 0:22:09
0:22:09
 0:19:27
0:19:27
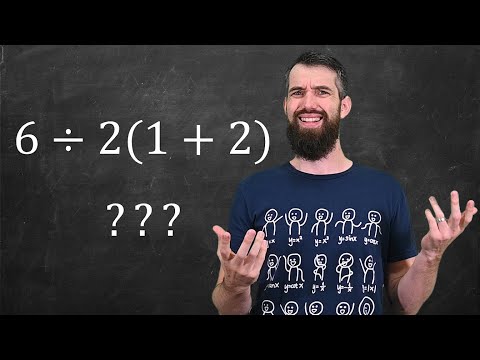 0:06:04
0:06:04
![[Discrete Mathematics] Midterm](https://i.ytimg.com/vi/8LGzMw1P0Xo/hqdefault.jpg) 0:44:06
0:44:06
 0:02:54
0:02:54
 0:09:46
0:09:46
 0:09:29
0:09:29
![[Discrete Mathematics] Midterm](https://i.ytimg.com/vi/_8ABr2Zkfog/hqdefault.jpg) 0:33:46
0:33:46
 0:19:34
0:19:34
 0:00:28
0:00:28
 0:04:48
0:04:48
 0:00:19
0:00:19
 0:06:29
0:06:29
 0:08:57
0:08:57
 0:00:21
0:00:21