filmov
tv
Hausdorff topological spaces

Показать описание
In this video, we look at topological spaces which satisfy an extra "separation axiom". They are known as Hausdorff spaces, and they are interesting because the separation axiom ensures that limits, when they exist, are unique. We give examples of Hausdorff spaces, and also a non-Hausdorff space where limits are not unique. Finally, we talk about what it means for a property of spaces to be topological. We see that being Hausdorff is such a topological property.
What is Hausdorff Topological Space?
Topology Lecture 07: Hausdorff Spaces
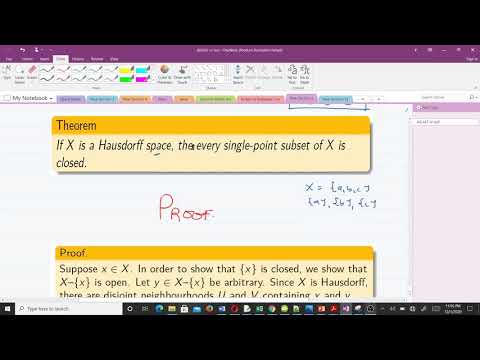
Hausdorff topological spaces
Hausdorff spaces
Intuitive Topology 7: Hausdorff
T1 – Spaces and Hausdorff Spaces - Chapter1videoLec-4
Metric Spaces | Lecture 36 | Hausdorff Property
Hausdorff spaces - Properties with proofs | Topology
Hausdroff Space | Examples | Topological Space | Higher mathematics | Ravina Tutorial
The Definition of Hausdorff topological spaces
Hausdorff Space
Hausdorff Example 1: Cofinite Topology
T2 space in topology | Hausdorff space in topology
Topology-Hausdorff Topological Spaces
Hausdorff space in topology in hindi/urdu | T2 space in topology in hindi/urdu |T2-space in topology
Hausdorff topological space | Wikipedia audio article
Compact and Hausdorff
Hausdorff Example 2: Quotient Space
Topology: Lecture 10: Hausdorff Spaces
Topology: Separation axioms Hausdorff space
Manifolds 3 | Hausdorff Spaces [dark version]
Algebraic Topology - 1 - Compact Hausdorff Spaces (a Review of Point-Set Topology)
Hausdorff Space in a Topological Space - Dr. Sujitha
T2 Topological Space#Hausdorff Space#Convergent Sequence in Hausdorff space
Комментарии
 0:04:43
0:04:43
 0:32:01
0:32:01
 0:16:05
0:16:05
 0:05:12
0:05:12
 0:13:52
0:13:52
 0:51:36
0:51:36
 0:08:38
0:08:38
 0:14:26
0:14:26
 0:13:33
0:13:33
 0:16:11
0:16:11
 0:09:56
0:09:56
 0:09:21
0:09:21
 0:06:28
0:06:28
 0:25:36
0:25:36
 0:05:17
0:05:17
 0:13:25
0:13:25
 0:15:12
0:15:12
 0:06:03
0:06:03
 0:28:19
0:28:19
 0:22:32
0:22:32
 0:09:11
0:09:11
 0:24:49
0:24:49
 0:05:08
0:05:08
 0:12:39
0:12:39