Algebraic Topology - 1 - Compact Hausdorff Spaces (a Review of Point-Set Topology)

This is mostly a review point set topology.

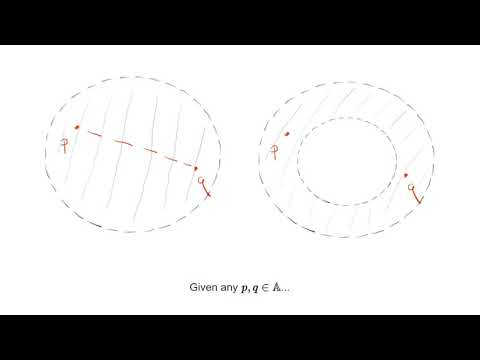
In general it is not true that a bijective continuous map is invertible (you need to worry about the inverse being continuous). In the case that your spaces are compact hausdorff this is true! We prove this in this video and review necessary facts along the way.

[mathstrek]

The proof of lemma 1 has a slight gap: it doesn't use the fact that A is closed in X. At around 11:15 we should extend the cover of A to a cover of X by adding the open set (X-A); the resulting open cover (of A) has a finite subcover. WLOG we can exclude the set (X-A) from this subcover.

[narutosaga]

YESSS!! I was looking for an Alg Top series!! Thank YOUUU 🙏🙏

[BiTCoRn]

Love the video but the constantly changing camera focus is very distracting.

[jholomorphic]

Thanks for these lectures. Could you please share the details of the recording setup?

[InfiniteQuest]

Perhaps a dumb question, but is there an example of a subset of a compact space that is not closed and not compact? It feels like the proof was just subsets of compact spaces are compact.

[taylordupuy]

We have a zulip chat too for this course. Send me an email if you want to join.