Properties of Symmetric Matrices

For Notes and Practice set WhatsApp @ 8130648819 or visit our Website

Join this channel to get access to perks:

Real Analysis: Interior points, limit points, open sets, closed sets, bounded sets, connected sets, compact sets, completeness of R. Power series (of real variable), Taylor's series, radius and interval of convergence, term-wise differentiation and integration of power series.

Jam 2019 MCQ MA Real Analysis University Entrance Exam DU
Properities of Symmetric Matrix
(i) In a symmetric matrix the elements above the principal diagonal and the element below the principal diagonal are
same.
(ii) The Square null matrix,diagonal matrix,scalar matrix and identity matrix are always symmetric matrices.
(iii) Every symmetric matrix is necessarily be square matrix.
(iv) Symmetric matrix may be singular or non-singular according as its determinant is zero or non-zero,
respectively.
(v) If A is symmetric matrix,then kA is also symmetric matrix for any scalar k.
(vi) If A and B are symmetric matrices of same order.Then,λ_1 A±λ_2 B are also symmetric matrices for scalars λ_1
and λ_2.
(vii) If A and B are both symmetric matrices of same order.Then,AB is symmetric matrix if AB=BA,i.e.A and B are
commute.
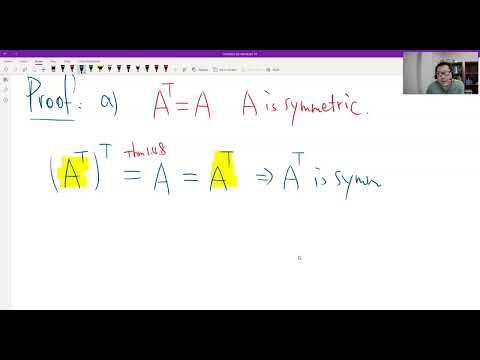
(viii) If A be any square matix.Then,AA^T and A^T A both will be symmetric matrix.
(ix) If A and B are symmetric matrices of same order.Then,AB+BA must be symmetric matrix.
Explanation: (AB+BA)^T=(AB)^T+(BA)^T
=B^T A^T+A^T B^T
=BA+AB=AB+BA
(x) If A is symmetric matrix,then all positive intergral powers of A are symmetric matrices.
(xi) If A is any square matrix,then A+A^T is always symmetric matrix.