filmov
tv
Solution of Elliptic Equation - Part 5 | 9 Mesh Squares | Laplace Equation
Показать описание
Partial Differential Equations are fundamental in engineering mathematics, and they play a crucial role in modeling and solving various engineering problems. In this video, we'll focus on one particular type of PDE, the Elliptic Equation, and show you how to solve it using a numerical method called the 9 Mesh Squares method.
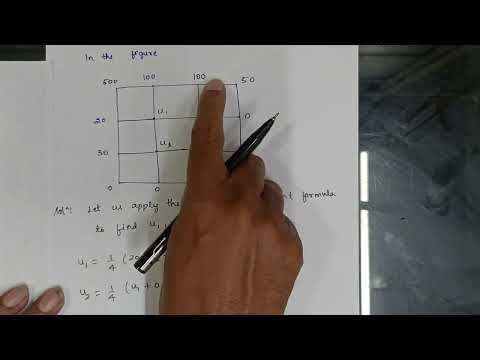
We'll start by introducing the concept of Elliptic Equations and their significance in engineering mathematics. Then, we'll discuss the numerical solution of PDEs and how the 9 Mesh Squares method can be used to solve the Elliptic Equation.
We'll provide a step-by-step demonstration of the 9 Mesh Squares method, which involves dividing the region of interest into a grid of squares and solving the equations at each grid point. This technique is also known as the Finite Difference Method, and we'll discuss its advantages and limitations.
We'll provide examples of different types of Elliptic Equations and show you how to apply the 9 Mesh Squares method to solve them. We'll also discuss how to handle boundary conditions and provide tips for optimizing the solution.
By the end of this video, you'll have a solid understanding of the numerical solution of Elliptic Equations using the 9 Mesh Squares method. Whether you're an engineering student or a practicing engineer, this video will be an excellent resource for you to learn and apply this technique to solve engineering problems.
So, if you're ready to take your engineering mathematics skills to the next level, watch this tutorial and learn how to solve the Elliptic Equation using the 9 Mesh Squares method.
[ 📐 Watch Next ]
Solution of Elliptic Equation 16 Mesh Squares
Solution of Elliptic Equation 9 Mesh Squares
[ ⭐ 21MAt31 Solved Module Question Paper]
[ ⭐ 21mat31 Important - Passing Package]
[ 📐 Playlists ]
[21MAT31] - Engineering Mathematics 3
#vtu #21mat31 #module4 #engineeringmathematics3 #NumericalSolution #pde #examples #mathematicstutor
We'll start by introducing the concept of Elliptic Equations and their significance in engineering mathematics. Then, we'll discuss the numerical solution of PDEs and how the 9 Mesh Squares method can be used to solve the Elliptic Equation.
We'll provide a step-by-step demonstration of the 9 Mesh Squares method, which involves dividing the region of interest into a grid of squares and solving the equations at each grid point. This technique is also known as the Finite Difference Method, and we'll discuss its advantages and limitations.
We'll provide examples of different types of Elliptic Equations and show you how to apply the 9 Mesh Squares method to solve them. We'll also discuss how to handle boundary conditions and provide tips for optimizing the solution.
By the end of this video, you'll have a solid understanding of the numerical solution of Elliptic Equations using the 9 Mesh Squares method. Whether you're an engineering student or a practicing engineer, this video will be an excellent resource for you to learn and apply this technique to solve engineering problems.
So, if you're ready to take your engineering mathematics skills to the next level, watch this tutorial and learn how to solve the Elliptic Equation using the 9 Mesh Squares method.
[ 📐 Watch Next ]
Solution of Elliptic Equation 16 Mesh Squares
Solution of Elliptic Equation 9 Mesh Squares
[ ⭐ 21MAt31 Solved Module Question Paper]
[ ⭐ 21mat31 Important - Passing Package]
[ 📐 Playlists ]
[21MAT31] - Engineering Mathematics 3
#vtu #21mat31 #module4 #engineeringmathematics3 #NumericalSolution #pde #examples #mathematicstutor
0:22:58
75. Solution of Elliptic Equation | Laplace Equation | Problem#1 | Complete Concept
0:04:40
Lecture 3 Finite Difference Method to Solve Elliptic Equation
0:20:31
76. Solution of Elliptic Equation | Laplace Equation | Problem#2 | Complete Concept
0:15:31
78. Solution of Elliptic Equation | Poisson's Equation | Problem#3 | Complete Concept
0:15:38
Solution of Elliptic Equation - Part 1 | 16 Mesh Squares | Laplace Equation
0:26:23
Solution of Elliptic Equation | Poisson's Equation | Numerical method | Full Concept | square m...
0:04:35
PDE Classification: Elliptic, Parabolic, and Hyperbolic
0:13:43
Chapter 10.03: Lesson: Elliptic PDEs: Gauss-Seidel Method
0:18:30
79. Solution of Elliptic Equation by Relaxation Method | Problem#1 | Most Important
0:10:03
Numerical solution of Partial Differential equations
0:21:45
Numerical solution of Partial Differential Equations
0:19:25
Numerical Elliptic PDE Part 4 Solving Temperature Distribution of Elliptic PDE (Example #1)
0:08:26
Lecture 13 02 Elliptic PDEs - Finite difference method
0:09:18
Chapter 10.03: Lesson: Direct method: Numerical Solution of Elliptic PDEs
0:25:37
Class 07 Part 01 Elliptic Equation
0:23:09
Numerical solution of Partial Differential Equations
0:06:50
Classification of PDEs into Elliptic, Hyperbolic and Parabolic
0:06:29
Solution of Elliptic Equations - Problems
0:38:47
Solution of Elliptic Equation - Part 2 | 16 Mesh Squares | Laplace Equation
0:17:55
Laplace's Equation and Poisson's Equation
0:17:39
But what is a partial differential equation? | DE2
0:16:08
Liebmann's Iteration Process | Elliptic Equation | Solution of Laplace equation | Problem in Ta...
0:10:35
How to solve numerical solution of PDE best and simple example
0:11:18
Solution of Laplace Equation with 9 mesh squares || Numerical Methoda || Dr Prashant Patil
Комментарии