Lecture 3 Finite Difference Method to Solve Elliptic Equation

preview_player
Показать описание
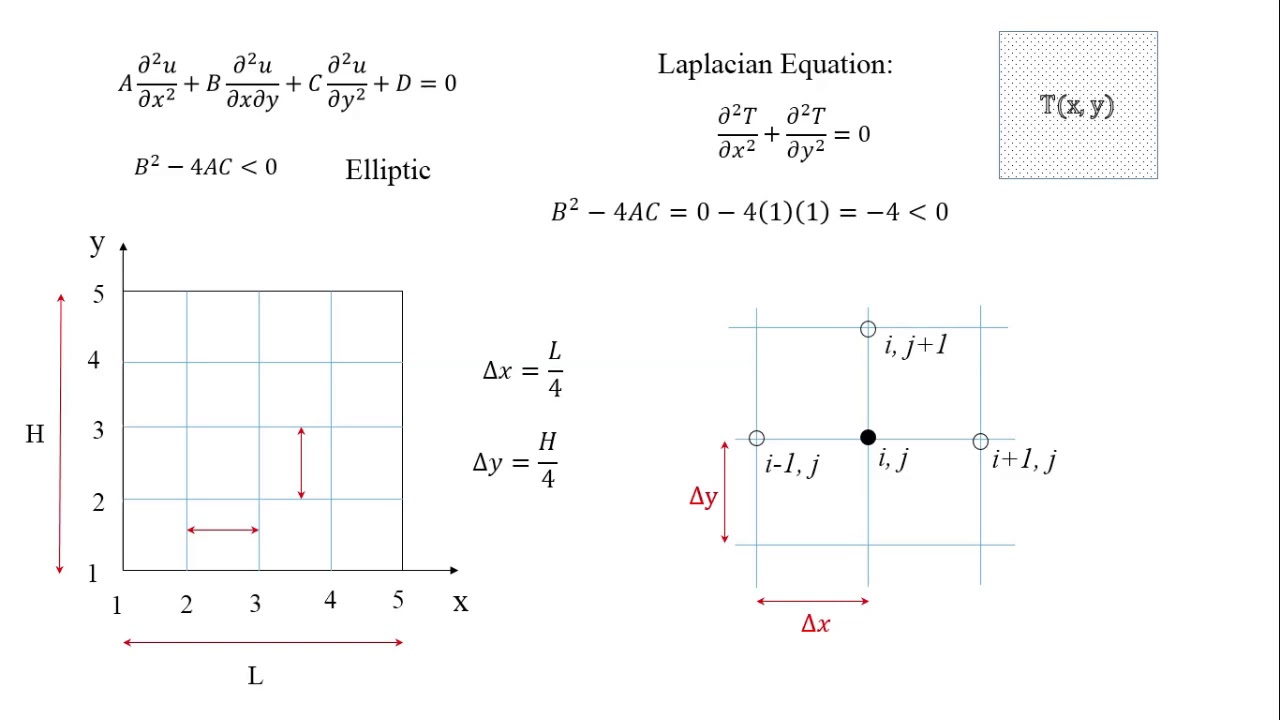
In this lecture, implementation of the finite difference method (FDM) to solve elliptic equation is covered. In order to have more clarity about this method, an example of steady-state heat conduction in a two-dimensional domain is considered. This lecture covers only the implementation part. The solution part using Gauss-Seidel method will be covered in Lecture 4.
  1. Vipul Patel
  2. finite difference method
  3. elliptic equation
  4. Gauss-Seidel method
  5. Numerical methods
  6. Laplace equation
Рекомендации по теме
Lecture 3 Finite 0:04:40

Lecture 3 Finite Difference Method to Solve Elliptic Equation

Lecture 3 Part 0:51:10

Lecture 3 Part 2: Finite-Difference Approximations

MIT Numerical Methods 0:13:21

MIT Numerical Methods for PDE Lecture 3: Finite Difference for 2D Poisson's equation

MIT Numerical Methods 0:06:20

MIT Numerical Methods for PDE Lecture 3: Finite Difference 2D Matlab Demo

Intro to Finite 0:01:56

Intro to Finite Differences 3 Finite Differences with Partial Differential Equations

Finite Differences 0:08:35

Finite Differences

PDE | Finite 0:06:49

PDE | Finite differences: introduction

MIT Numerical Methods 0:14:42

MIT Numerical Methods for PDE Lecture 3: Mapping for 2D finite difference

Finite Difference Method: 0:11:03

Finite Difference Method: (3) Derivatives

7.3.3-ODEs: Finite Difference 0:14:13

7.3.3-ODEs: Finite Difference Method

Finite Differences using 0:22:18

Finite Differences using MATLAB | Lecture 3 | ICFDM

3 Finite Difference 0:12:45

3 Finite Difference Method -FDM

Lecture 10 (Part 0:39:45

Lecture 10 (Part 3) Finite Difference Time Domain Method

Lecture 03- Numerical 0:29:03

Lecture 03- Numerical methods: Finite Difference Approach

Lecture 3: Approaches 0:12:50

Lecture 3: Approaches to derive finite difference schemes

Week 3 - 1:14:46

Week 3 - Finite-difference approximations II

Lecture 02 Part 0:06:24

Lecture 02 Part 3: Finite Difference for Heat Equation, 2016 Numerical Methods for PDE

8.2.3-PDEs: Explicit Finite 0:12:11

8.2.3-PDEs: Explicit Finite Difference Method for Parabolic PDEs

Approximating the Jacobian: 0:08:54

Approximating the Jacobian: Finite Difference Method for Systems of Nonlinear Equations

Lecture -- Introduction 0:13:29

Lecture -- Introduction to Two-Dimensional Finite-Difference Method

Finite Differences - 0:12:56

Finite Differences - The Easy Way to Solve Differential Equations

Lecture -- Introduction 0:26:35

Lecture -- Introduction to 1D Finite Difference Method

The Finite Difference 0:08:34

The Finite Difference Method

Why greatest Mathematicians 0:00:38

Why greatest Mathematicians are not trying to prove Riemann Hypothesis? || #short #terencetao #maths

Комментарии
Автор

how does this work if delta x does not equal delta y?

JafacaksWasTaken