filmov
tv
Solution of Elliptic Equation - Part 2 | 16 Mesh Squares | Laplace Equation

Показать описание
In engineering mathematics, partial differential equations are used to model many physical systems. However, solving these equations can be challenging, especially for complex systems. One way to tackle this problem is to use numerical methods to obtain approximate solutions. In this video, we'll demonstrate how to use 16 mesh squares to solve elliptic equations numerically.
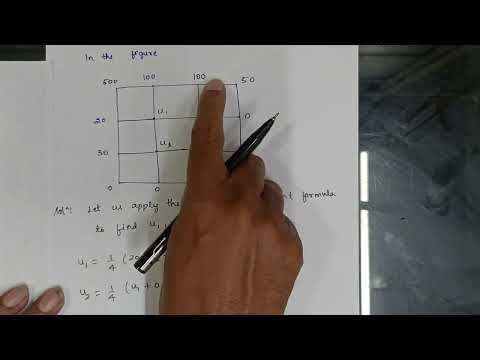
We'll start by introducing elliptic equations and explaining why they're important in engineering. Then, we'll show you how to discretize the equations using the finite difference method. We'll divide the domain into a grid of 16 mesh squares and approximate the derivatives using central difference formulas.
Next, we'll explain how to set up the linear system of equations that represents the discretized problem. We'll use matrix algebra to solve the system and obtain the numerical solution.
To help you understand the process, we'll provide step-by-step examples, including boundary conditions and source terms. We'll also discuss how to handle non-uniform grids and refine the mesh to improve the accuracy of the solution.
By the end of this video, you'll have a solid understanding of how to use 16 mesh squares to obtain numerical solutions of elliptic equations. Whether you're a student of engineering mathematics or a practicing engineer, this technique will be a valuable tool in your toolkit.
So, if you're ready to learn how to solve elliptic equations numerically using 16 mesh squares, watch this tutorial and take your engineering mathematics skills to the next level.
[ 📐 Watch Next ]
Solution of Elliptic Equation 16 Mesh Squares
Solution of Elliptic Equation 9 Mesh Squares
[ ⭐ 21MAt31 Solved Module Question Paper]
[ ⭐ 21mat31 Important - Passing Package]
[ 📐 Playlists ]
[21MAT31] - Engineering Mathematics 3
#vtu #21mat31 #module4 #engineeringmathematics3 #NumericalSolution #pde #examples #mathematicstutor
We'll start by introducing elliptic equations and explaining why they're important in engineering. Then, we'll show you how to discretize the equations using the finite difference method. We'll divide the domain into a grid of 16 mesh squares and approximate the derivatives using central difference formulas.
Next, we'll explain how to set up the linear system of equations that represents the discretized problem. We'll use matrix algebra to solve the system and obtain the numerical solution.
To help you understand the process, we'll provide step-by-step examples, including boundary conditions and source terms. We'll also discuss how to handle non-uniform grids and refine the mesh to improve the accuracy of the solution.
By the end of this video, you'll have a solid understanding of how to use 16 mesh squares to obtain numerical solutions of elliptic equations. Whether you're a student of engineering mathematics or a practicing engineer, this technique will be a valuable tool in your toolkit.
So, if you're ready to learn how to solve elliptic equations numerically using 16 mesh squares, watch this tutorial and take your engineering mathematics skills to the next level.
[ 📐 Watch Next ]
Solution of Elliptic Equation 16 Mesh Squares
Solution of Elliptic Equation 9 Mesh Squares
[ ⭐ 21MAt31 Solved Module Question Paper]
[ ⭐ 21mat31 Important - Passing Package]
[ 📐 Playlists ]
[21MAT31] - Engineering Mathematics 3
#vtu #21mat31 #module4 #engineeringmathematics3 #NumericalSolution #pde #examples #mathematicstutor
Комментарии
 0:15:38
0:15:38
 0:22:58
0:22:58
 0:20:31
0:20:31
 0:15:31
0:15:31
 0:10:03
0:10:03
 0:26:23
0:26:23
 0:18:30
0:18:30
 0:16:08
0:16:08
 0:06:29
0:06:29
 0:23:38
0:23:38
 0:44:55
0:44:55
 0:24:31
0:24:31
 0:38:47
0:38:47
 0:09:08
0:09:08
 0:22:39
0:22:39
 0:04:40
0:04:40
 0:21:45
0:21:45
 0:23:21
0:23:21
 0:13:56
0:13:56
 0:23:09
0:23:09
 0:24:10
0:24:10
 0:29:08
0:29:08
 0:04:35
0:04:35
 0:58:08
0:58:08