filmov
tv
Quotient Rule Made Easier (NancyPi)

Показать описание
MIT grad shows an easy way to use the Quotient Rule to differentiate rational functions and a shortcut to remember the formula. The calculus Quotient Rule derivative rule is one of the derivative rules for differentiation. It's used to take the derivative of a rational function. To skip ahead: 1) For an easy way to remember the Quotient Rule formula, skip to time 0:21. 2) For an example of how to use the Quotient Rule to take the derivative of a fraction or quotient of functions (rational function), skip to 1:41. This video is a basic introduction to the Quotient Rule for taking derivatives in calculus. Nancy formerly of MathBFF explains the steps.
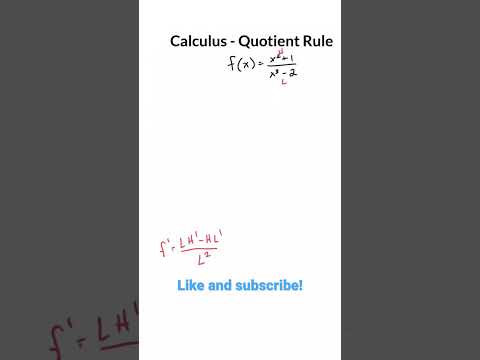
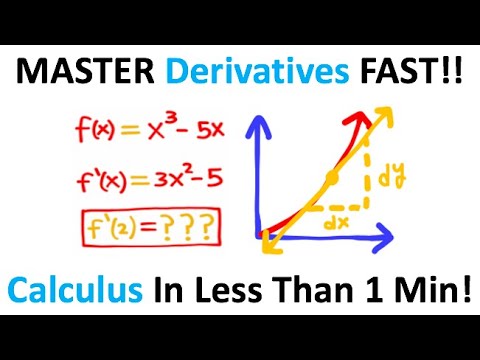
The Quotient Rule (calculus) tells you how to find the derivative of rational functions (a fraction, or one function divided by another function). The formal definition (textbook definition) of the Quotient Rule is often unnecessarily complex and intimidating.
There is a memory trick, or mnemonic, for how to remember the Quotient Rule formula. All you need to remember is the song "LO dee-HI minus HI dee-LO, over LO LO," where "dee" means the "derivative of." "HI" means your top function in the numerator, and "LO" means your bottom function in the denominator.
In other words, multiply the bottom function times the derivative of the top function MINUS the top function times the derivative of the bottom function, then DIVIDED by the bottom function times itself. After you differentiate the function with the Quotient Rule, remember to simplify the expression as much as possible using algebra.
The Quotient Rule (calculus) tells you how to find the derivative of rational functions (a fraction, or one function divided by another function). The formal definition (textbook definition) of the Quotient Rule is often unnecessarily complex and intimidating.
There is a memory trick, or mnemonic, for how to remember the Quotient Rule formula. All you need to remember is the song "LO dee-HI minus HI dee-LO, over LO LO," where "dee" means the "derivative of." "HI" means your top function in the numerator, and "LO" means your bottom function in the denominator.
In other words, multiply the bottom function times the derivative of the top function MINUS the top function times the derivative of the bottom function, then DIVIDED by the bottom function times itself. After you differentiate the function with the Quotient Rule, remember to simplify the expression as much as possible using algebra.
Комментарии
 0:03:14
0:03:14
 0:16:36
0:16:36
 0:11:56
0:11:56
 0:14:17
0:14:17
 0:01:25
0:01:25
 0:02:13
0:02:13
 0:05:02
0:05:02
 0:08:13
0:08:13
 0:14:30
0:14:30
 0:25:50
0:25:50
 0:00:57
0:00:57
 0:11:13
0:11:13
 0:09:03
0:09:03
 0:00:58
0:00:58
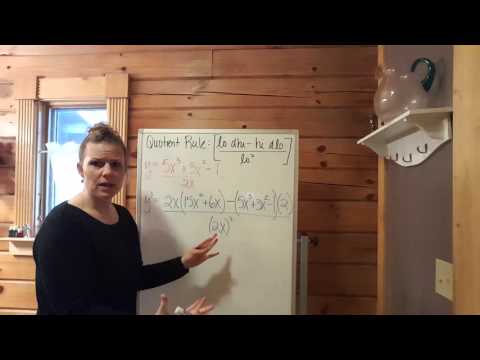 0:05:13
0:05:13
 0:08:59
0:08:59
 0:04:59
0:04:59
 0:15:37
0:15:37
 0:00:30
0:00:30
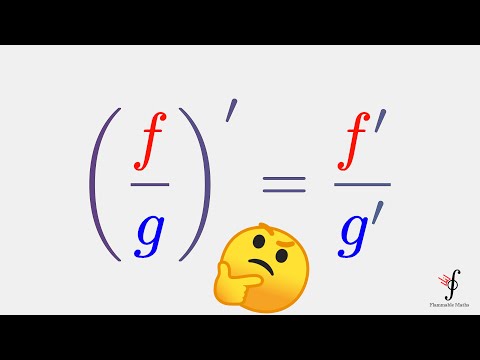 0:14:30
0:14:30
 0:05:18
0:05:18
 0:14:55
0:14:55
 0:05:25
0:05:25
 0:00:31
0:00:31