filmov
tv
Find Two Differential Equations Whose Solution is y = A*e^x + B*cos(x)
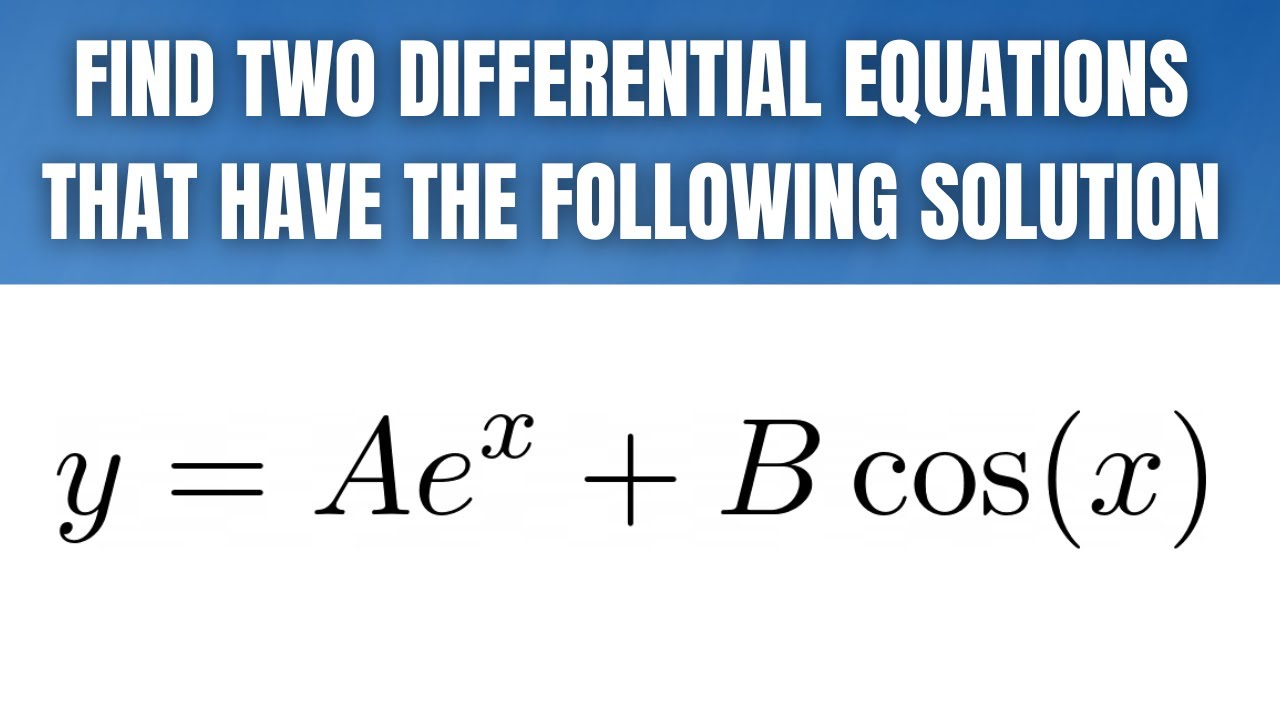
Показать описание
In this video we have a solution of a differential equation y = Ae^x + Bcos(x). We are asked to find TWO differential equations who have this as a solution. This is a fun problem. I hope this helps someone.
If you enjoyed this video please consider liking, sharing, and subscribing.
There are several ways that you can help support my channel:)
************Udemy Courses(Please Use These Links If You Sign Up!)*************
Abstract Algebra Course
Advanced Calculus Course
Calculus 1 Course
Calculus 2 Course
Calculus 3 Course
Calculus 1 Lectures with Assignments and a Final Exam
Calculus Integration Insanity
Differential Equations Course
Differential Equations Lectures Course (Includes Assignments + Final Exam)
College Algebra Course
How to Write Proofs with Sets Course
How to Write Proofs with Functions Course
Trigonometry 1 Course
Trigonometry 2 Course
Statistics with StatCrunch Course
Math Graduate Programs, Applying, Advice, Motivation
Daily Devotionals for Motivation with The Math Sorcerer
Thank you:)
If you enjoyed this video please consider liking, sharing, and subscribing.
There are several ways that you can help support my channel:)
************Udemy Courses(Please Use These Links If You Sign Up!)*************
Abstract Algebra Course
Advanced Calculus Course
Calculus 1 Course
Calculus 2 Course
Calculus 3 Course
Calculus 1 Lectures with Assignments and a Final Exam
Calculus Integration Insanity
Differential Equations Course
Differential Equations Lectures Course (Includes Assignments + Final Exam)
College Algebra Course
How to Write Proofs with Sets Course
How to Write Proofs with Functions Course
Trigonometry 1 Course
Trigonometry 2 Course
Statistics with StatCrunch Course
Math Graduate Programs, Applying, Advice, Motivation
Daily Devotionals for Motivation with The Math Sorcerer
Thank you:)
Find Two Differential Equations Whose Solution is y = A*e^x + B*cos(x)
Ex: Find Two Exponential Function Solutions to a Differential Equation
Calculus 2 | Find an Equation of the Curve Using Differential Equations
How to determine the general solution to a differential equation
Method of Undetermined Coefficients - Nonhomogeneous 2nd Order Differential Equations
Undetermined Coefficients: Solving non-homogeneous ODEs
How to form Ordinary Differential equations 004
Physics Students Need to Know These 5 Methods for Differential Equations
Differential Equations: eigensolution technique illustrated for 2x2 and 3x3 case, 9-9-24
Verifying solutions to differential equations | AP Calculus AB | Khan Academy
How to Solve Constant Coefficient Homogeneous Differential Equations
Second Order Linear Differential Equations
Mixing Problems and Separable Differential Equations
Differential equations, a tourist's guide | DE1
Is Differential Equations a Hard Class #shorts
Differential Equations - Non-Linear Systems - Finding Equilibrium Solutions
Finding Particular Solutions of Differential Equations Given Initial Conditions
Solving Second Order Differential Equations
Differential Equations - 31 - The Wronskian
Order And Degree Of Differential Equations | Differential Equation Class 12
This is why you're learning differential equations
Modeling population with simple differential equation | Khan Academy
5 simple unsolvable equations
How REAL Men Integrate Functions
Комментарии
 0:09:19
0:09:19
 0:04:23
0:04:23
 0:02:52
0:02:52
 0:02:03
0:02:03
 0:41:28
0:41:28
 0:12:44
0:12:44
 0:17:44
0:17:44
 0:30:36
0:30:36
 0:50:54
0:50:54
 0:05:52
0:05:52
 0:06:41
0:06:41
 0:25:17
0:25:17
 0:10:09
0:10:09
 0:27:16
0:27:16
 0:00:21
0:00:21
 0:02:48
0:02:48
 0:12:52
0:12:52
 0:32:54
0:32:54
 0:06:49
0:06:49
 0:01:55
0:01:55
 0:18:36
0:18:36
 0:07:40
0:07:40
 0:00:50
0:00:50
 0:00:35
0:00:35