filmov
tv
The Secret Behind -1 Factorial
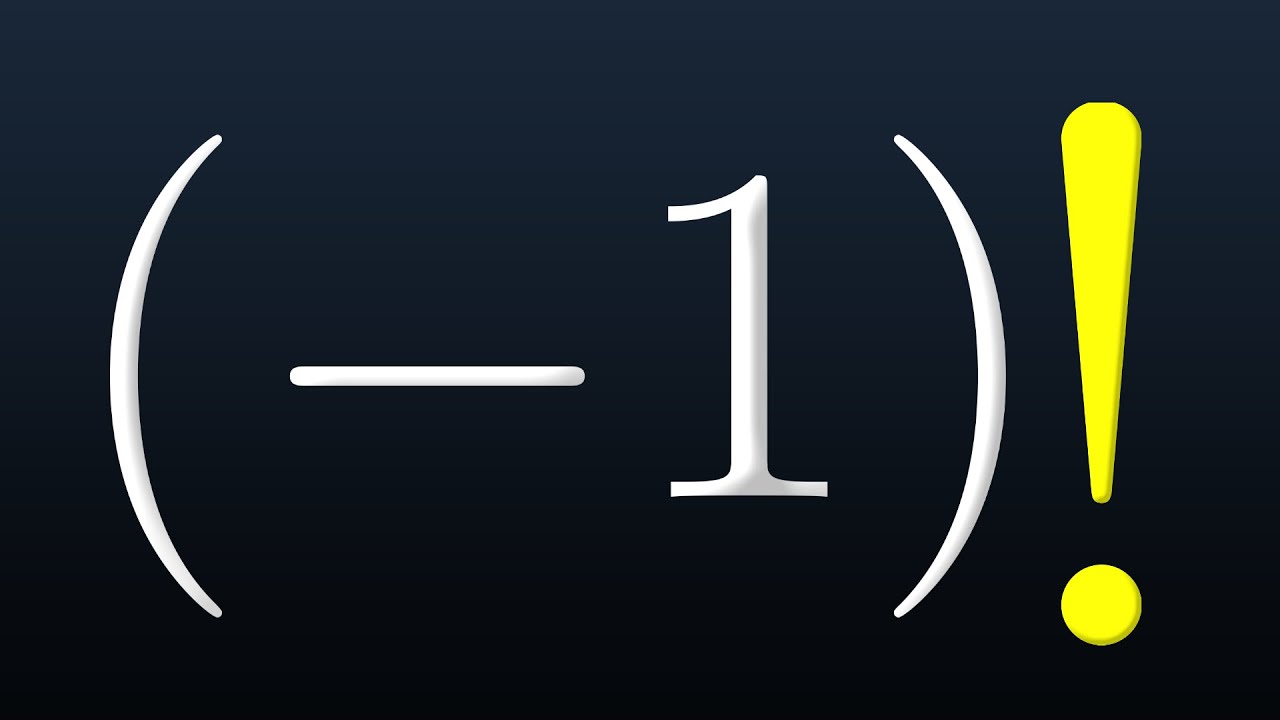
Показать описание
Dive into the mystery of -1 factorial! Explore advanced math topics like integrals and complex numbers as we tackle this perplexing question. Meet the gamma function, the key to extending factorials beyond positive integers. But there's a twist—calculus shows the integral diverges to infinity. Is -1! factorial really infinity, or is it more complex? Unlock the secrets with analytic continuation and decode Wolfram Alpha's intriguing output.
🙏Support me by becoming a channel member!
#math #brithemathguy #gamma
Disclaimer: This video is for entertainment purposes only and should not be considered academic. Though all information is provided in good faith, no warranty of any kind, expressed or implied, is made with regards to the accuracy, validity, reliability, consistency, adequacy, or completeness of this information. Viewers should always verify the information provided in this video by consulting other reliable sources.
🙏Support me by becoming a channel member!
#math #brithemathguy #gamma
Disclaimer: This video is for entertainment purposes only and should not be considered academic. Though all information is provided in good faith, no warranty of any kind, expressed or implied, is made with regards to the accuracy, validity, reliability, consistency, adequacy, or completeness of this information. Viewers should always verify the information provided in this video by consulting other reliable sources.
The Secret Behind -1 Factorial
Explaining Why 0 Factorial = 1... #shorts
How Real Men Calculate Factorials
How to Take the Factorial of Any Number
What’s 52 factorial ?
|i Factorial| You Won't Believe The Outcome
Prove that 0!=1 #factorial
Zero Factorial - Numberphile
Mathematics Using Python (Advance): Sir Sourish Sarkar
what is infinity factorial?
What is the factorial of -½?
why 0!=1 in 30 Seconds. (Shortest 0 factorial proof) #shorts
#Why 0 Factorial is 1 ?#short#shorts
What is the factorial of the square root of negative 1? #shorts
What Is The Factorial Of 1/2? SURPRISING (1/2)! = (√π)/2
Guess! The value of (-1) factorial
Why 1 factorial = 1
what is i factorial?
Big Factorials - Numberphile
a nice factorial problem
Factorials Explained!
The Highest-Scoring Move in Scrabble
I Found Out What Infinity Factorial Is
The Inverse Factorial? (Using Stirling's Approximation!)
Комментарии
 0:05:03
0:05:03
 0:00:48
0:00:48
 0:00:38
0:00:38
 0:26:31
0:26:31
 0:00:33
0:00:33
 0:08:24
0:08:24
 0:00:33
0:00:33
 0:07:36
0:07:36
 1:48:14
1:48:14
 0:00:22
0:00:22
 0:12:46
0:12:46
 0:00:30
0:00:30
 0:00:31
0:00:31
 0:00:14
0:00:14
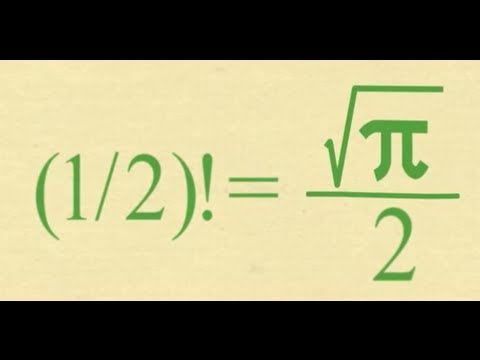 0:04:55
0:04:55
 0:01:30
0:01:30
 0:01:00
0:01:00
 0:07:56
0:07:56
 0:12:27
0:12:27
 0:00:37
0:00:37
 0:11:17
0:11:17
 0:00:58
0:00:58
 0:04:25
0:04:25
 0:09:31
0:09:31