filmov
tv
Algebra maths Olympiad question

Показать описание
we are going to show you how to solve #math,#olympiad,#problems
math olympiad questions,math olympiad preparation,Nice Olympiad maths problem ,olympiad mathematics
➡️Video link
➡️ Video Chapters
0:00 introduction
02:33 laws of surds and indices
06:56 how to expand
math olympiad problems,math olympiad,math problems,math olympiad questions,math olympiad question,math olympiad problem,olympiad mathematics,math olympiad preparation,math olympiad algebra problem,mathematical olympiad,#challenging math problems,nice algebra problem,algebra problem,math olympiad training,olympiad math problems,exponential problems,algebra 1,#algebra 2,algebra problems,learn how to solve exponential equation quickly,solve exponential equation,laws of exponents,exponential equations,exponential equation,math olympics,a nice algebra problem,sat algebra problem on exponents,a nice olympiad exponential problem,exponential growth word problem,math olympiad algebra,nice exponent problem,non-routine math problems,negative #exponent problem,exponential word problems,exponents and powers,olympiad math,olympiad question,sat math,quadratic equations,pre math Algebra mathematics Algebra maths Olympiad quest ion Maths olympiad questions Surds and indices math a nticssurds and indices for ssc cglAlg ebra maths Olympiad questionsurds and indices questionsmath anticssurds and indices for ssc cgl Algebra maths Olympiad question surds and indices tricks
math olympiad questions,math olympiad preparation,Nice Olympiad maths problem ,olympiad mathematics
➡️Video link
➡️ Video Chapters
0:00 introduction
02:33 laws of surds and indices
06:56 how to expand
math olympiad problems,math olympiad,math problems,math olympiad questions,math olympiad question,math olympiad problem,olympiad mathematics,math olympiad preparation,math olympiad algebra problem,mathematical olympiad,#challenging math problems,nice algebra problem,algebra problem,math olympiad training,olympiad math problems,exponential problems,algebra 1,#algebra 2,algebra problems,learn how to solve exponential equation quickly,solve exponential equation,laws of exponents,exponential equations,exponential equation,math olympics,a nice algebra problem,sat algebra problem on exponents,a nice olympiad exponential problem,exponential growth word problem,math olympiad algebra,nice exponent problem,non-routine math problems,negative #exponent problem,exponential word problems,exponents and powers,olympiad math,olympiad question,sat math,quadratic equations,pre math Algebra mathematics Algebra maths Olympiad quest ion Maths olympiad questions Surds and indices math a nticssurds and indices for ssc cglAlg ebra maths Olympiad questionsurds and indices questionsmath anticssurds and indices for ssc cgl Algebra maths Olympiad question surds and indices tricks
Комментарии
 0:07:26
0:07:26
 0:08:40
0:08:40
 0:01:26
0:01:26
 0:09:15
0:09:15
 0:07:32
0:07:32
 0:01:54
0:01:54
 0:02:51
0:02:51
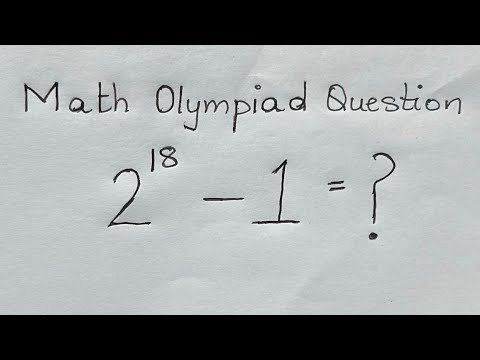 0:03:21
0:03:21
 0:10:31
0:10:31
 0:00:52
0:00:52
 0:10:49
0:10:49
 0:01:00
0:01:00
 0:00:33
0:00:33
 0:15:56
0:15:56
 0:03:01
0:03:01
 0:02:24
0:02:24
 0:08:15
0:08:15
 0:07:50
0:07:50
 0:09:19
0:09:19
 0:00:28
0:00:28
 0:07:27
0:07:27
 0:08:13
0:08:13
 0:08:36
0:08:36
 0:04:00
0:04:00