filmov
tv
Olympiad Mathematics Question || Solving Olympiad Exponential Equation

Показать описание
In this solution to Olympiad mathematics question, you will learn how to solve tough exponential equations with easy. You will equally be introduced to how you can solve for the imaginary roots of any exponential equation applying Euler's equation and other mathematical rules. You will gain a complete understanding of the Euler's identity otherwise know as the most beautiful equation.
Here, you will also learn about the factorization method of solving quadratic equations step-by-step.
#exponents #exponentialequations #onlinemathstv
Here, you will also learn about the factorization method of solving quadratic equations step-by-step.
#exponents #exponentialequations #onlinemathstv
Norway Math Olympiad Question | You should be able to solve this!
Luxembourg - Math Olympiad Question | You should know this trick
A Nice Olympiad Exponential Multiplication Problem #short #olympiad #mathematics #maths #exponents
Math Olympiad Question | Equation solving | You should learn this trick to pass the exam
A Nice Math Olympiad Exponential Equation 3^x = X^9
Math Olympiad Question | You should know how to solve this!!
Thailand | Math Olympiad Question | Nice Algebra Equation
Maths Olympiad | A Tricky Maths Olympiad Questions | Algebra Problem |
Can You Solve This? olympiad math radical simplification | Square root i + Square root -i =?
Solving the hardest question of a British Mathematical Olympiad
France - Math Olympiad Question | An Algebraic Expression | You should be able to solve this!
Math Olympiad 3^m–2^m=65 | Math Olympiad Problems | Algebra
Mexico - A Nice Math Olympiad Exponential Problem
Math Olympiad Question | Indices - Equation Solving | A Must Known Trick
Germany - Math Olympiad Exponential Problem.
A beautiful international math olympiad problem
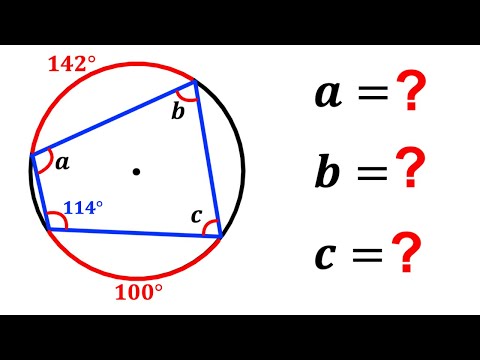
Can you calculate the angles a, b, and c? | (Circle) | #math #maths | #geometry
The unexpectedly hard windmill question (2011 IMO, Q2)
Poland - Math Olympiad Question | You should be able to solve this!
One of the HARDEST International Math Olympiad Question
Math Olympiad Practice
UK - Math Olympiad Question | You should be able to solve this without calculators!!
Russia | Math Olympiad Question | You should know this trick!!
New Zealand - Math olympiad Question
Комментарии
 0:03:21
0:03:21
 0:02:51
0:02:51
 0:00:52
0:00:52
 0:01:54
0:01:54
 0:02:34
0:02:34
 0:02:24
0:02:24
 0:01:26
0:01:26
 0:08:03
0:08:03
 0:08:04
0:08:04
 0:11:26
0:11:26
 0:08:40
0:08:40
 0:10:49
0:10:49
 0:08:36
0:08:36
 0:02:44
0:02:44
 0:04:45
0:04:45
 0:01:00
0:01:00
 0:08:20
0:08:20
 0:16:03
0:16:03
 0:00:50
0:00:50
 0:10:51
0:10:51
 0:01:00
0:01:00
 0:03:20
0:03:20
 0:08:01
0:08:01
 0:01:12
0:01:12