Lecture 16: The Min/Max Theorem and Bolzano's Intermediate Value Theorem

preview_player
Показать описание
MIT 18.100A Real Analysis, Fall 2020
Instructor: Dr. Casey Rodriguez

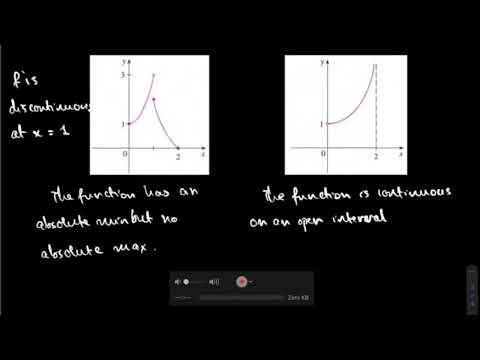
We prove some of the most useful tools of calculus: the Min/Max theorem or the Extreme Value Theorem (EVT) and the Intermediate Value Theorem (IVT). Is every hypothesis in these theorems required?

License: Creative Commons BY-NC-SA

  1. MIT OpenCourseWare
  2. EVT
  3. Extreme Value Theorem
  4. IVT
  5. Intermediate Value Theorem
  6. Min/Max Theorem
Рекомендации по теме
Lecture 16: The 1:08:24

Lecture 16: The Min/Max Theorem and Bolzano's Intermediate Value Theorem

Courant Fischer Min-Max 0:08:16

Courant Fischer Min-Max Theorem

A Uniform Min-Max 0:19:40

A Uniform Min-Max Theorem with Applications in Cryptography

The minimax theorem. 0:01:01

The minimax theorem.

MINIMAX THEOREM informal 0:04:23

MINIMAX THEOREM informal illustration

Math-S400: Lecture XIII 1:03:48

Math-S400: Lecture XIII - Berge's maximisation theorem

How much does 0:00:34

How much does B.TECH pay?

M 08 04: 0:03:53

M 08 04: extreme value theorem (Weierstrass)

3-2-1 Technique to 0:00:59

3-2-1 Technique to Improve Memory 🔥| Mind Blowing Way to increase Brain Power 💪 #shorts #reels #tips...

Proof of the 0:09:39

Proof of the Min-max theorem, part 1

Alpha beta pruning 0:08:29

Alpha beta pruning in artificial intelligence with example.

Minimax Algorithm in 0:12:29

Minimax Algorithm in Game Playing | Artificial Intelligence

Minimax Theorem 0:13:47

Minimax Theorem

Absolute Maximum and 0:11:24

Absolute Maximum and Minimum Values of Multivariable Functions - Calculus 3

Calculus 3 Lecture 3:38:16

Calculus 3 Lecture 13.8: Finding Extrema of Functions of 2 Variables (Max and Min)

Poset (Minimal and 0:13:39

Poset (Minimal and Maximal Elements)

😁 Playing 🐍Snake🐍 0:00:47

😁 Playing 🐍Snake🐍 game on calculator 😜 [official video] #shorts #viral #casio

Min max theorem 0:28:21

Min max theorem & Cauchy interlacing

JEE Aspirants ka 0:00:12

JEE Aspirants ka Sach 💔 #JEE #JEEMain #Shorts

Quadratic Equations IIT 0:00:50

Quadratic Equations IIT Questions No 11 ( X Class)

Anushka Mam got 0:00:53

Anushka Mam got angry on student #pwians #physicswallah #shorts #ytshortsindia

Lecture 16 - 0:13:04

Lecture 16 - Part 1: Extreme Value Theorem and Critical Points || Calculus 1

Can you solve 0:00:57

Can you solve this 150 years old puzzle? #shorts

A Second Course 1:21:21

A Second Course in Algorithms (Lecture 10: The Minimax Theorem & Algorithms for Linear Programmi...

Комментарии
Автор

Hey self-learners! Be aware of a minor typo at 55:18. It should be b_(n-1) not b_(n-2). FANTASTIC LECTURE MIT ocw!

nicolasg.b.
Автор

41:55 love how it "pains [him]" to say the definition of continuity is the fact that you can draw a function without picking up the chalk since that's what we all learned in high school. Frankly I like the real analysis definition a lot more too, but I can't really think of any counterexamples of the "don't pick up your chalk" example, aside from the fact that it isn't exactly rigorous. Great way to introduce the concept to those not as interested in math.

nathanielthomas
Автор

To do the negation he used a direct proof with contradiction

Jay-tzb