Evaluating for secant using even and odd properties

👉 Learn how to evaluate trigonometric functions using trigonometric identities. Trigonometric identities are equalities that involve trigonometric functions. We will focus on the cofunction identities and even-odd identities.

The cofunction identities property states that the value of the trigonometric function of an angle is equal to the value of the cofunction of the complement of the angle. The cofunctions are sine and cosine, tangent and cotangent, cosecant and secant. For example: sin (90 - x) = cos x; tan (90 - x) = cot x, etc

The even/odd identities are trigonometric identities used to evaluate negative angles of even or odd trigonometric functions. Note that for odd functions: f(-x) = -f(x) and for even functions f(-x) = f(x). Sine and tangent with their reciprocal functions are odd, while cosine with its reciprocal function are even. Thus, sin(-x) = -sin x; cos(-x) = cos x, etc.

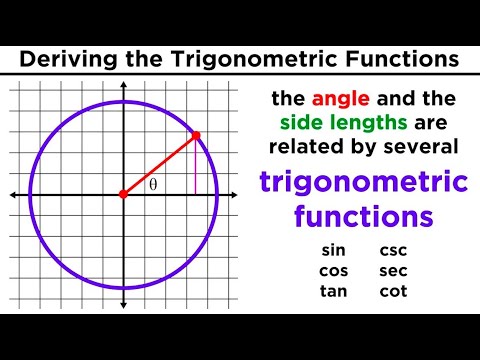
Other very important trigonometric identities are: tan x = sin x / cos x and cot x = cos x / sin x. With the knowledge of these identities, we can evaluate the trigonometric functions of angles given the value of the trigonometric functions of other (necessary) angles.

Organized Videos:
✅ Trigonometric Functions and The Unit Circle
✅ The Unit Circle | Learn About
✅ Points of the Unit Circle | Learn About
✅ Angles of the Unit Circle | Learn About
✅ Trigonometric Functions of the Unit Circle
✅ Find the Point on the Unit Circle
✅ Evaluate Trigonometric Functions Using the Unit Circle
✅ Evaluate the Six Trigonometric Functions Given and Angle
✅ Evaluate trigonometric functions using a calculator
✅ Evaluate trigonometric functions using identities

Connect with me:

#trig #unitcircle #brianmclogan