filmov
tv
Germany Math Olympiad Problem | A Very Nice Geometry Challenge

Показать описание
Germany Math Olympiad Problem | A Very Nice Geometry Challenge
MY OTHER CHANNELS
••••••••••••••••••••••••••••••••
--------------------------------------------------------------------------------
Become a member of this channel to get access of ULTIMATE MATH COURSE
(New video will be uploaded every week)
Join the channel to become a member
MY OTHER CHANNELS
••••••••••••••••••••••••••••••••
--------------------------------------------------------------------------------
Become a member of this channel to get access of ULTIMATE MATH COURSE
(New video will be uploaded every week)
Join the channel to become a member
Germany - Math Olympiad Problem | Be Careful!
Germany Math Olympiad Problem | Best Math Olympiad Problem | Geometry
Germany - Math Olympiad Exponential Problem.
Germany - Olympiad math exponential problem
Germany Math Olympiad Question | You should know this trick!
Germany Math Olympiad Problem | A Very Nice Geometry Challenge
Germany | Junior Maths Olympiad Questions | A nice algebra problem |
Germany Math Olympiad | How To Solve Germany Math Olympiad Problem.
Germany ll Can you solve this problem ll maths Olympiad
Unlocking the Secrets of Exponents: Germany's Math Olympiad Challenge!
Germany | Maths Olympiad | A tricky Algebra Maths Olympiad Problems |
Germany| Math Olympiad math problem| Can you pass this exam.
Germany Math Olympiad Problem. Easy Solution 👇
Germany - Math Olympiad Exponential Problem @Mamtamaam
Germany | Math Olympiad | Exponential Problem
Germany | Can you solve this ? | A Nice Math Olympiad Problem
Germany |A nice Math Olympiad Problem | Ca you sove this x=? & y=?
Germany - Math Olympiad Question | The BEST Trick
Germany | A nice Math Olympiad Exponential Simplification | You Should Master this Trick | #maths
Germany maths olympiad |a nice maths algebra problem| how to find the values of a and b
Germany| A Math Olympiad problem| Exponential question| Can you solve this.
A Nice Math Olympiad Exponential Equation 3^x = X^9
How Solve a Math Germany Olympiad Problem? | Mathematical Olympiad
Germany - Math Olympiad Challenge | Solve for integers a,b
Комментарии
 0:10:06
0:10:06
 0:14:56
0:14:56
 0:04:45
0:04:45
 0:06:29
0:06:29
 0:11:10
0:11:10
 0:14:50
0:14:50
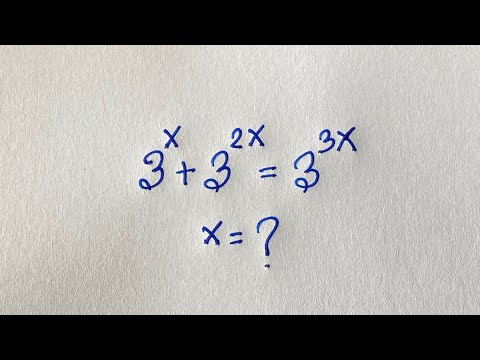 0:05:00
0:05:00
 0:13:55
0:13:55
 0:09:41
0:09:41
 0:02:41
0:02:41
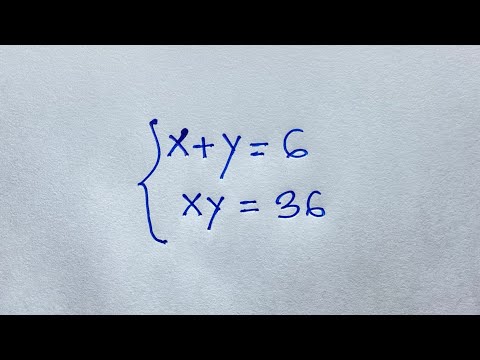 0:11:18
0:11:18
 0:07:55
0:07:55
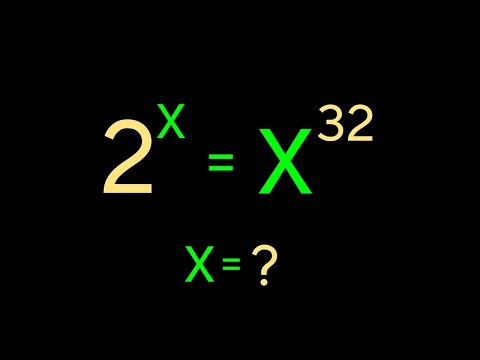 0:03:05
0:03:05
 0:08:04
0:08:04
 0:10:19
0:10:19
 0:01:07
0:01:07
 0:12:53
0:12:53
 0:10:37
0:10:37
 0:08:46
0:08:46
 0:05:49
0:05:49
 0:07:43
0:07:43
 0:02:34
0:02:34
 0:15:02
0:15:02
 0:04:25
0:04:25