filmov
tv
Deriving the Arc Length and Area of a Cycloid! [ Cut Version ]
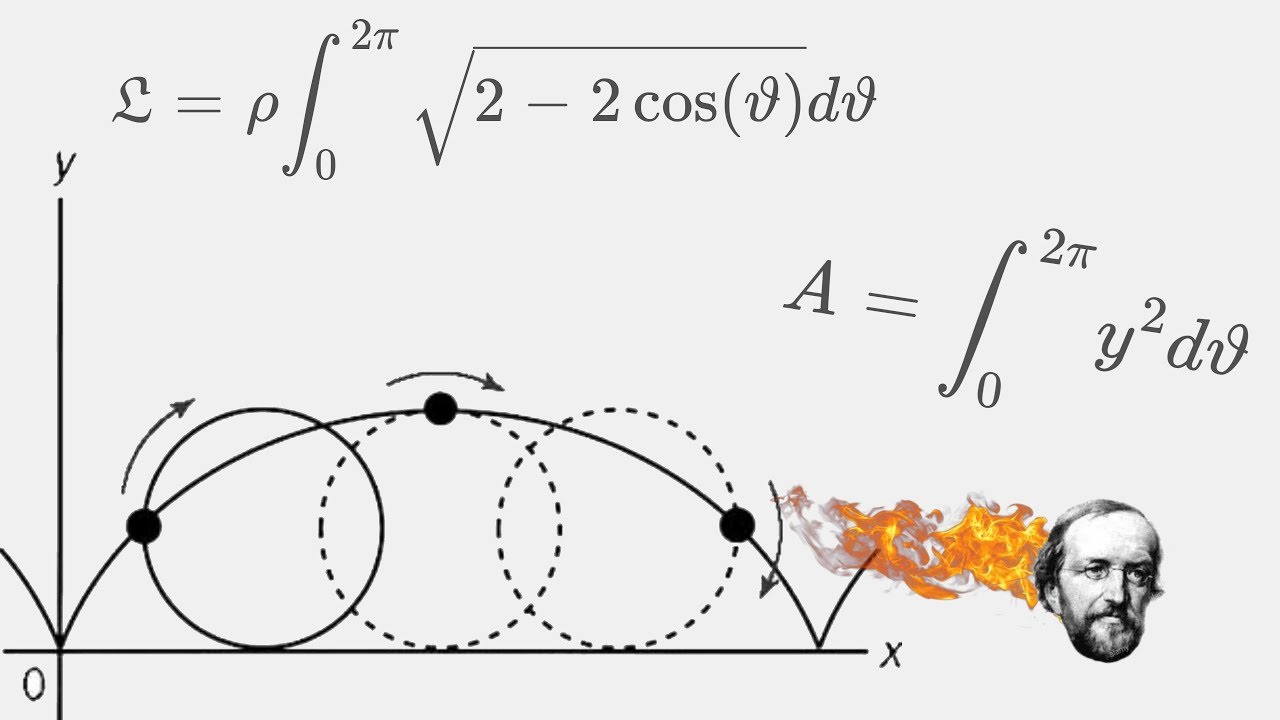
Показать описание
Help me create more free content! =)
Here we go, have fun watching me doing trivial integrals :D Love ya mah bois and grills :)
Here we go, have fun watching me doing trivial integrals :D Love ya mah bois and grills :)
Arc Length (formula explained)
Arclength Formula | Derivation & Ex: Circumference of a Circle
Arc Length Calculus Problems,
Arc length intro | Applications of definite integrals | AP Calculus BC | Khan Academy
Arc Length of a Circle Formula - Sector Area, Examples, Radians, In Terms of Pi, Trigonometry
Deriving the Arc Length Formula in Calculus
Introduction to Arc Length Derivation and Example
Arc Length Derivation and First Example
Find Arc Length (Calculus) #maths #calculus
How long is a curve?? The Arclength Formula in 3D
I want to show you how to prove the arc length formula
Deriving the Arc Length in Cartesian and Polar Coordinates
How do we Find the Length of an Arc? | Circles | Don't Memorise
Arc Length (Formula)
arc measure vs arc length
Arc Length of Parametric Curves
How to Find the Arc Length in a Circle
GCSE Maths - Area of a Sector and Length of an Arc of a Circle (Circles Part 3) #108
Why Students Struggle With Arc Length and How to Help
Derivation and Example of Arc length for Polar Form of an Equation
Deriving the Formula for Arc Length
Calculus 2: Ch 18 Arc Length (of Curves) (1 of 18) What is Arc Length?
Finding Arc Lengths | GCSE Maths 2025
arc length formula #math #radian #degree #shorts
Комментарии
 0:07:57
0:07:57
 0:10:13
0:10:13
 0:30:47
0:30:47
 0:06:21
0:06:21
 0:15:57
0:15:57
 0:16:37
0:16:37
 0:07:17
0:07:17
 0:03:08
0:03:08
 0:01:39
0:01:39
 0:07:10
0:07:10
 0:01:25
0:01:25
 0:13:48
0:13:48
 0:03:35
0:03:35
 0:01:11
0:01:11
 0:00:42
0:00:42
 0:12:34
0:12:34
 0:01:01
0:01:01
 0:05:39
0:05:39
 0:09:57
0:09:57
 0:06:28
0:06:28
 0:05:09
0:05:09
 0:03:20
0:03:20
 0:00:54
0:00:54
 0:00:25
0:00:25