filmov
tv
VECTOR Curl F and Divergence F example (PART-2)

Показать описание
In this video explaining VECTOR Curl F and Divergence F.
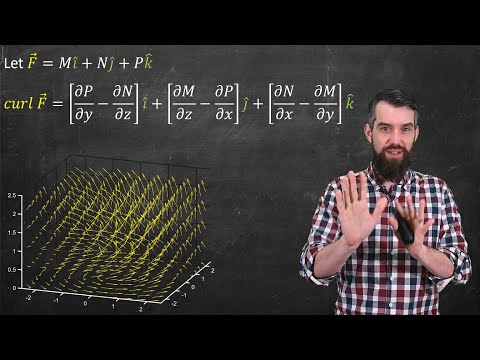
Divergence and curl are two important vector operators in vector calculus.
Curl: The curl of a vector field is a vector quantity that represents the rotation or circulation of the field at a particular point. It is defined as the cross product of the del operator with the vector field F and is denoted by ∇ x F.
#vectordivergence #vectorcurl
18MAT21 MODULE 1:Vector Calculus
18MAT21 MODULE 2:Differential Equation higher order
18MAT21 MODULE 3: Partial differential equations
18MAT21 MODULE 4: Infiinite series & Power series solution
18MAT21 MODULE 5: Numerical methods
18MAT11 Module1: Differential Calculus1
18MAT11 Module2: differential Calculus2
18MAT11 Module4: Ordinary differential equations
Linear Algebra: 18MAT11 MODULE 5
LAPLACE TRANSFORM : 18MAT31
Fourier Transforms Z-transform : 18MAT31 & 17MAT31
Fourier Series: 18MAT31 & 17MAT31
Calculus of Variation & Numerical Methods 18MAT31
Numerical Methods ODE's: 18MAT31 & 17MAT41
Joint Probability & Sampling Theory: 18MAT41 & 17MAT41
Probability Distributions: 18MAT41 & 17MAT41
Calculus of Complex Functions: 18MAT41 & 17MAT41
Curve fitting & Statistical Method 18MAT41 17MAT31
Divergence and curl are two important vector operators in vector calculus.
Curl: The curl of a vector field is a vector quantity that represents the rotation or circulation of the field at a particular point. It is defined as the cross product of the del operator with the vector field F and is denoted by ∇ x F.
#vectordivergence #vectorcurl
18MAT21 MODULE 1:Vector Calculus
18MAT21 MODULE 2:Differential Equation higher order
18MAT21 MODULE 3: Partial differential equations
18MAT21 MODULE 4: Infiinite series & Power series solution
18MAT21 MODULE 5: Numerical methods
18MAT11 Module1: Differential Calculus1
18MAT11 Module2: differential Calculus2
18MAT11 Module4: Ordinary differential equations
Linear Algebra: 18MAT11 MODULE 5
LAPLACE TRANSFORM : 18MAT31
Fourier Transforms Z-transform : 18MAT31 & 17MAT31
Fourier Series: 18MAT31 & 17MAT31
Calculus of Variation & Numerical Methods 18MAT31
Numerical Methods ODE's: 18MAT31 & 17MAT41
Joint Probability & Sampling Theory: 18MAT41 & 17MAT41
Probability Distributions: 18MAT41 & 17MAT41
Calculus of Complex Functions: 18MAT41 & 17MAT41
Curve fitting & Statistical Method 18MAT41 17MAT31
Комментарии
 0:15:42
0:15:42
 0:15:36
0:15:36
 0:13:02
0:13:02
 0:13:11
0:13:11
 0:06:27
0:06:27
 0:08:26
0:08:26
 0:03:54
0:03:54
 0:10:25
0:10:25
 1:09:10
1:09:10
 0:28:09
0:28:09
 0:07:47
0:07:47
 0:05:22
0:05:22
 0:10:40
0:10:40
 1:11:50
1:11:50
 0:05:25
0:05:25
 0:12:21
0:12:21
 0:06:43
0:06:43
 0:18:55
0:18:55
 0:31:14
0:31:14
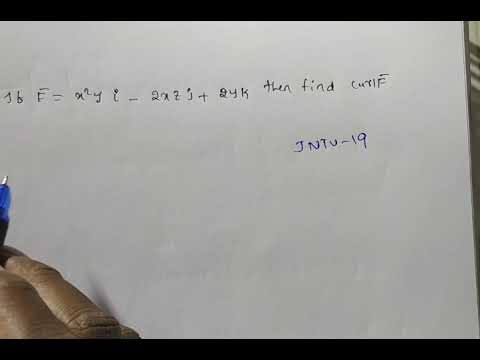 0:02:57
0:02:57
 0:18:26
0:18:26
 0:02:18
0:02:18
 0:08:09
0:08:09
 0:11:12
0:11:12