filmov
tv
The Gradient Vector Field

Показать описание
One prominent example of a vector field is the Gradient Vector Field. Given any scalar, multivariable function f: R^n\to R, we can get a corresponding vector field that has a precise geometrical meaning: the vectors point in the direction of maximal increase of the function.
MY VECTOR CALCULUS PLAYLIST:
OTHER COURSE PLAYLISTS:
OTHER PLAYLISTS:
► Learning Math Series
►Cool Math Series:
BECOME A MEMBER:
MATH BOOKS & MERCH I LOVE:
SOCIALS:
MY VECTOR CALCULUS PLAYLIST:
OTHER COURSE PLAYLISTS:
OTHER PLAYLISTS:
► Learning Math Series
►Cool Math Series:
BECOME A MEMBER:
MATH BOOKS & MERCH I LOVE:
SOCIALS:
The Gradient Vector Field
What Does the Gradient Vector Mean Intuitively?
Geometric Meaning of the Gradient Vector
Divergence and curl: The language of Maxwell's equations, fluid flow, and more
Gradients and Partial Derivatives
How To Find The Directional Derivative and The Gradient Vector
Gradient Vector Field Example -- Calculus 3, Vector Calculus
What is a gradient? Explained in under one minute
Gradient, Divergence & Curl
Gradient
The Gradient Operator in Vector Calculus: Directions of Fastest Change & the Directional Derivat...
What is Gradient? #calculus
Vectors, Vector Fields, and Gradients | Multivariable Calculus
This Downward Pointing Triangle Means Grad Div and Curl in Vector Calculus (Nabla / Del) by Parth G
Gradient Fields in Vector Calculus
Div, Grad, and Curl: Vector Calculus Building Blocks for PDEs [Divergence, Gradient, and Curl]
Gradient Vector Fields
Gradient Vectors (KristaKingMath)
Gradient, Divergence and Curl Concepts | Physics |
Gradient and contour maps
Are all vector fields the gradient of a potential? ... and the Helmholtz Decomposition
14.6 Directional derivative and gradient | Anas Abu Zahra
Vector Fields, Divergence, and Curl
Find the Gradient Vector Field of f(x,y)=x^3y^5
Комментарии
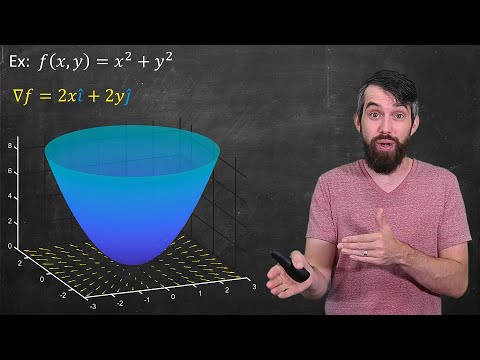 0:02:18
0:02:18
 0:02:14
0:02:14
 0:14:51
0:14:51
 0:15:42
0:15:42
 0:05:24
0:05:24
 0:28:30
0:28:30
 0:00:42
0:00:42
 0:00:49
0:00:49
 0:08:12
0:08:12
 0:05:31
0:05:31
 0:15:04
0:15:04
 0:00:58
0:00:58
 0:20:26
0:20:26
 0:12:52
0:12:52
 0:05:32
0:05:32
 0:13:02
0:13:02
 0:07:53
0:07:53
 0:04:57
0:04:57
 0:10:25
0:10:25
 0:06:17
0:06:17
 0:16:36
0:16:36
 0:31:55
0:31:55
 0:15:36
0:15:36
 0:03:22
0:03:22