filmov
tv
When can we 'divide' in a linear congruence? (Number theory basics)
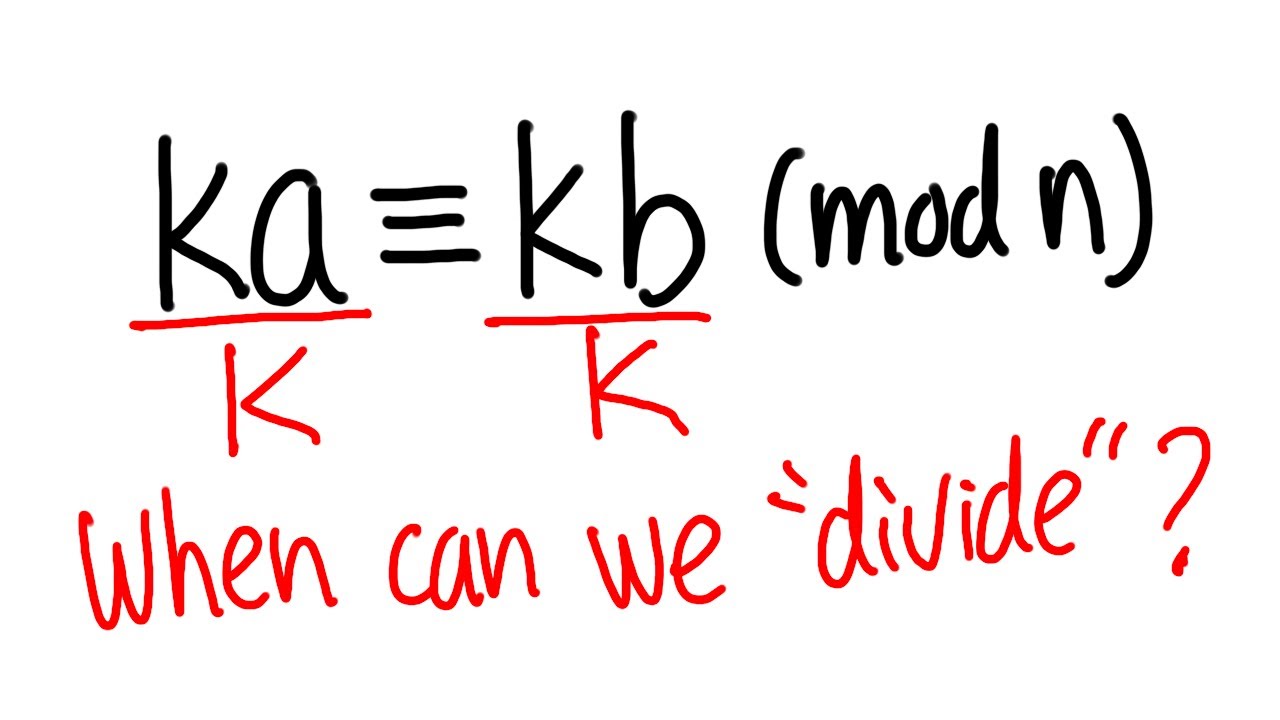
Показать описание
When can we divide both sides of congruence by the same number?
discrete math, number theory, abstract algebra,
discrete math, number theory, abstract algebra,
When can we 'divide' in a linear congruence? (Number theory basics)
Why can't you divide by zero? - TED-Ed
Actually, you CAN divide by zero.
How Do I Know When to Divide or Multiply in Fraction Word Problems? : Multiplication Tips
What happens when you divide by zero on a mechanical calculator?
Determine When to Multiply or Divide When Solving Word Problems
I Learned How to Divide by Zero (Don't Tell Your Teacher)
Why do we have to flip the sign when we divide or multiply by negative one - Cool Math
#fun #maths #algebra #logarithm #for #you #youtubeshorts !
Answer: Can we divide leptons and quarks into even smaller particles?
The Sample Variance: Why Divide by n-1?
How to Divide a Variable by a Number
The REAL reason you can't divide by zero
Why can't you divide by 0? Animation vs Math
What if we divide any number with zero? | Dividing by Zero Explained
Divide a Whole Number by a Fraction
Divide and check your answer
Why do we divide by n-1 and not n? | shown with a simple example | variance and sd
Divisions - Learn to Divide with our Monkey Friends
Variance and Standard Deviation: Why divide by n-1?
How to Multiply and Divide in Standard Form (Part 3/4) #25
How to Divide Big Numbers : Math Solutions
Learn how to divide radicals
Word Problems: Should I Add, Subtract, Multiply, or Divide?
Комментарии
 0:09:15
0:09:15
 0:04:51
0:04:51
 0:03:52
0:03:52
 0:01:34
0:01:34
 0:00:40
0:00:40
 0:05:58
0:05:58
 0:07:36
0:07:36
 0:02:32
0:02:32
 0:00:59
0:00:59
 0:04:45
0:04:45
 0:06:53
0:06:53
 0:01:41
0:01:41
 0:01:39
0:01:39
 0:00:45
0:00:45
 0:03:45
0:03:45
 0:00:26
0:00:26
 0:04:29
0:04:29
 0:10:14
0:10:14
 0:03:53
0:03:53
 0:13:47
0:13:47
 0:06:12
0:06:12
 0:02:35
0:02:35
 0:01:49
0:01:49
 0:07:48
0:07:48