filmov
tv
The Logistic Map: Attractors, Bifurcation, and Chaos (Part 1 of 2)

Показать описание
We explore the logistic map, a quadratic mapping that is often used as the exemplar for how chaotic behavior can arise from a simple equation. We examine its fixed points and attractors at various parameters, including period doubling and the onset of chaos. We also dive into the details of the logistic map's associated bifurcation diagram, and the Feigenbaum constant.
Original background music uses Emulator II V, Synclavier V, and SQ-80 V from Arturia.
This is Part 1 of a two-part series. Part 2 featuring complex numbers is out now:
And please consider supporting this channel so we may bring you more cultural content:
Original background music uses Emulator II V, Synclavier V, and SQ-80 V from Arturia.
This is Part 1 of a two-part series. Part 2 featuring complex numbers is out now:
And please consider supporting this channel so we may bring you more cultural content:
This equation will change how you see the world (the logistic map)
The Logistic Map: Attractors, Bifurcation, and Chaos (Part 1 of 2)
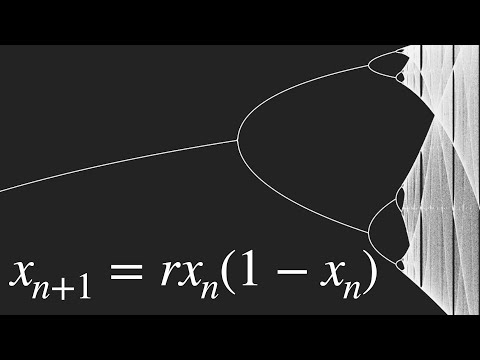
Logistic Map: Bifurcation Diagram from the movement of the initial points towards the attractors
Explaining the Bifurcation Diagram for the Logistic Map
Bifurcation diagram of the Logistic map.
Chaos of the Logistic Map
Logistic Map, Part 1: Period Doubling Route to Chaos
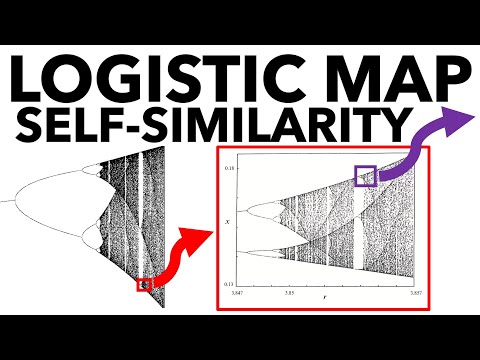
Zoom into the bifurcation diagram for the logistic map (chaotic map)
Logistic Map, Part 2: Bifurcation Diagram and Self-Similarity
Logistic Map, Part 3: Bifurcation Point Analysis | Bottlenecks in Maps, Intermittency Chaos
Logistic Map Bifurcation Diagram Progression
Bifurcation diagram of a logistic Map
Logistic map bifurcation diagram animation
Chaos: The Science of the Butterfly Effect
Logistic map bifurcation diagram
Logistic Map Part 2: Complex Numbers and 3D Bifurcation
Logistic Map
Logistic Map zoom at the boundary between order and chaos
Matlab code for the Bifurcation Diagram of the Logistic Map
Bifurcation Diagram (Logistic Map)
Logistic map. Simple Examples of Bifurcations.
The Sound of the Logistic Map
logistic map and bifurcation and chaos
Is the Logistic Map hiding in the Mandelbrot Set? | #SoME3
Комментарии
 0:18:39
0:18:39
 0:05:48
0:05:48
 0:02:07
0:02:07
 0:24:01
0:24:01
 0:00:41
0:00:41
 0:01:01
0:01:01
 0:17:18
0:17:18
 0:00:30
0:00:30
 0:15:19
0:15:19
 0:20:35
0:20:35
 0:01:00
0:01:00
 0:00:31
0:00:31
 0:00:37
0:00:37
 0:12:51
0:12:51
 0:00:37
0:00:37
 0:09:44
0:09:44
 0:00:16
0:00:16
 0:00:23
0:00:23
 0:06:21
0:06:21
 0:00:35
0:00:35
 0:32:21
0:32:21
 0:01:12
0:01:12
 0:30:31
0:30:31
 0:12:14
0:12:14