Logistic Map Part 2: Complex Numbers and 3D Bifurcation

preview_player
Показать описание
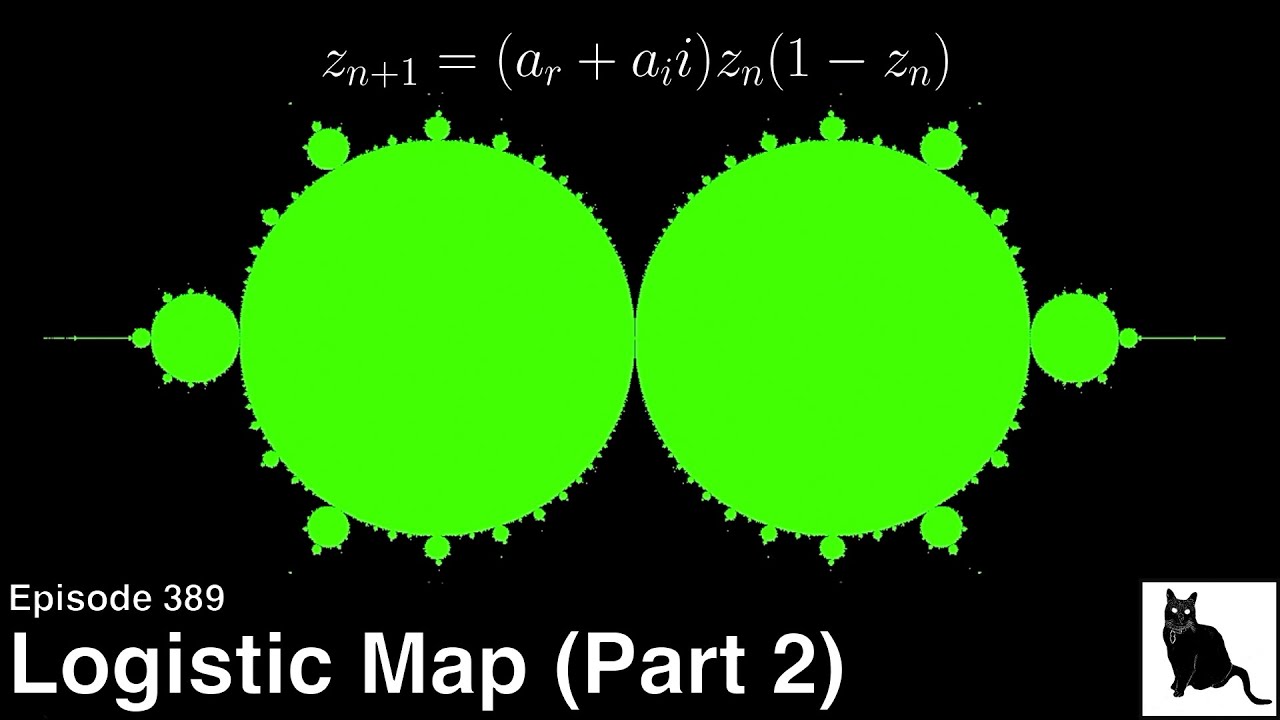
We continue our exploration with of the logistic map by looking at its behavior with complex coefficients. In particular we focus on attractors, period double, and chaos as the emerge on the complex plane. If you have not already seen Part 1 of this series, we recommend checking that out first.

Chapters:
00:23 Recap
01:33 Programming the logistic map for complex numbers
02:55 Exploring the complex attractor plot of the logistic map
06:54 Setting up a 3D bifurcation plot
07:25. Exploring the 3D bifurcation plot

Background music by Amanda Chaudhary:
Fibonacci rhythmic patterns using Kiltratrick Audio Carbon Sequencer and Yamaha RX5 drum machine; processed using Qu-Bit Prism and Strymon StarLab reverb. Additional music via original patch made in Arturia Pigments.

Please subscribe to this channel for more mathematical and cultural content coming out regularly, and please consider supporting this channel so we may bring you more cultural content:
  1. CatSynth TV
  2. logistic map
  3. complex numbers
  4. bifurcation diagram
  5. mandelbrot set
  6. quadratic map
Рекомендации по теме
Logistic Map Part 0:09:44

Logistic Map Part 2: Complex Numbers and 3D Bifurcation

Logistic Map, Part 0:15:19

Logistic Map, Part 2: Bifurcation Diagram and Self-Similarity

This equation will 0:18:39

This equation will change how you see the world (the logistic map)

The Logistic Map: 0:05:48

The Logistic Map: Attractors, Bifurcation, and Chaos (Part 1 of 2)

The Feigenbaum Constant 0:18:55

The Feigenbaum Constant (4.669) - Numberphile

Simple rules, complex 0:06:14

Simple rules, complex result: Logistic map bifurcations

Dynamical Systems And 0:09:46

Dynamical Systems And Chaos: Bifurcations: Part II (Logistic Map) Summary

Logistic Map zoom 0:00:23

Logistic Map zoom at the boundary between order and chaos

Online Refresher Course 3:05:50

Online Refresher Course on AI & Machine Learning Mastery | CFDET IIT (BHU) Varanasi | 07 Dec 202...

Logistic Map Superimposed 0:00:36

Logistic Map Superimposed upon its Bifurcation Diagram

The (Discrete) Logistic 0:33:43

The (Discrete) Logistic Map for population modeling

Introduction to Complexity: 0:00:43

Introduction to Complexity: Logistic Map Quiz Solution

Logistic Map, Part 0:20:35

Logistic Map, Part 3: Bifurcation Point Analysis | Bottlenecks in Maps, Intermittency Chaos

Bifurcation diagram of 0:00:41

Bifurcation diagram of the Logistic map.

Presentation on The 0:02:02

Presentation on The 1- and 2-Dimensional Logistic Maps

Foundational Concepts In 0:39:13

Foundational Concepts In Chaos Theory: An Explanation of Veritasium's Logistic Map Video

Introduction to Complexity: 0:11:10

Introduction to Complexity: Logistic Map

Existence of Period 0:22:26

Existence of Period 2 Solutions to Discrete Logistic Map

Logistic Map, Part 0:17:18

Logistic Map, Part 1: Period Doubling Route to Chaos

The Sound of 0:01:12

The Sound of the Logistic Map

Zoom into the 0:00:30

Zoom into the bifurcation diagram for the logistic map (chaotic map)

Logistic map bifurcation 0:00:37

Logistic map bifurcation diagram

Logistic map bifurcation 0:00:37

Logistic map bifurcation diagram animation

Chaos: The Science 0:12:51

Chaos: The Science of the Butterfly Effect

Комментарии
Автор

This is absolutely INCREDIBLE! Thank you so much for putting this together. It is wonderful.

TheParadoxOfParadox
Автор

Thank you for the fascinating video! Can I ask what you use to visualize the diagram? It's really cool that you can zoom in to that deep while keeping the resolution.

xinzhewu
Автор

great video! i have a question: the output of the complex logistics map is a complex number, but in the 3d bifurcation model you used only one dimension to represent a complex number, from what i understood of it. (you got 2 dimensions for the possible choices of complex parameters, and one dimension for the logistics map output, right?) did you project it into one of the coordinates?

violacosmo
Автор

so I’m imagining a scenario where you have a cobweb diagram with multiple curves. They all represent different r values maybe even different k values.

some number is entered into the first plot, and the number is returned, then it is submitted to the next curve, and then the next. Are there any good tools for understanding a sequence of operations like this?

Sagitarria