filmov
tv
Proof of Why Gradient of a Function is Perpendicular to its Level Curves
Показать описание
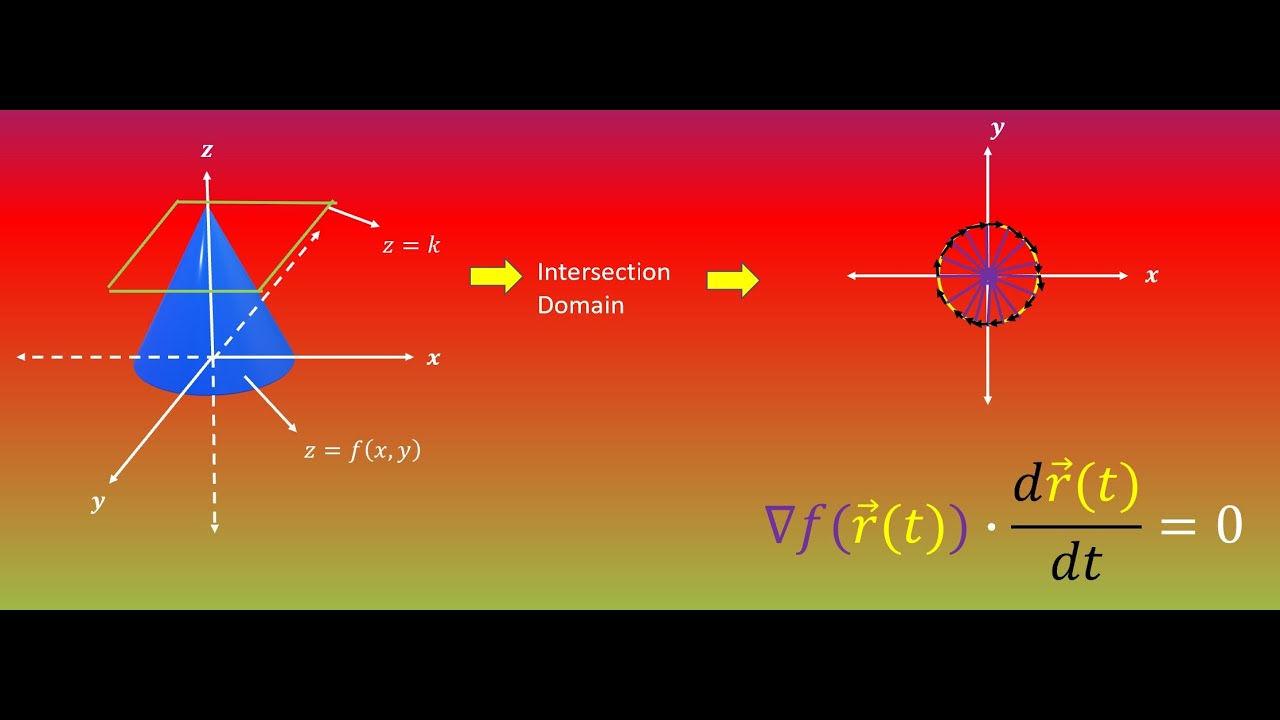
In this video, I take the familiar multivariable/vector calculus idea that the gradient of a 3D function is orthogonal to its level curves, prove this idea, and then try to extend the proof to higher dimensions of space.
Proof of Why Gradient of a Function is Perpendicular to its Level Curves
Why the gradient is the direction of steepest ascent
What Does the Gradient Vector Mean Intuitively?
Geometric Meaning of the Gradient Vector
Gradient
Facts about the Gradient Vector
The Gradient Vector Field
Line 2, Understanding Policy Gradient Proof
Mathematics P1 Nov 2005/ Grade 12 Final revision ( tricks and techniques)!@ zamokuhlemakhamba
1I Gradient theorem derivation
Gradient of Perpendicular Lines Proof
Why the gradient of a scalar function is always perpendicular to the surface. #gradient
Directional Derivatives | What's the slope in any direction?
Understanding Policy Gradient Proof - Introduction
How to prove the gradient question
Intro to Gradient Descent || Optimizing High-Dimensional Equations
Partial Derivatives and the Gradient of a Function
1 4 1 Gradient Descent Dyanmics Proof of Thm 6 part1
Line 4, Understanding Policy Gradient Proof
dagmult 3620 prove that curl of gradient of scalar field is zero 1
Gradient is perpendicular to the surface
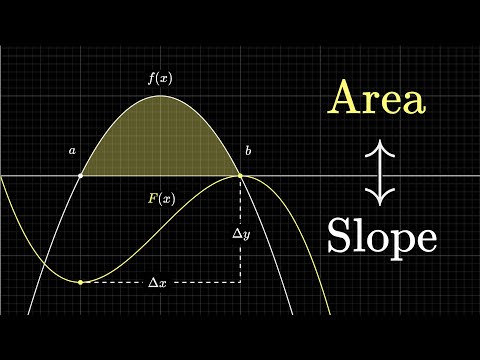
What does area have to do with slope? | Chapter 9, Essence of calculus
Vector Differential Opererator // Prove of gradient of sum of scalars
Gradient Descent with mathematical proof
Комментарии
 0:07:32
0:07:32
 0:10:32
0:10:32
 0:02:14
0:02:14
 0:14:51
0:14:51
 0:05:31
0:05:31
 0:09:47
0:09:47
 0:02:18
0:02:18
 0:01:46
0:01:46
 6:17:03
6:17:03
 0:04:37
0:04:37
 0:01:37
0:01:37
 0:07:15
0:07:15
 0:12:01
0:12:01
 0:08:30
0:08:30
 0:04:53
0:04:53
 0:11:04
0:11:04
 0:10:57
0:10:57
 0:10:46
0:10:46
 0:06:56
0:06:56
 0:00:31
0:00:31
 0:02:42
0:02:42
 0:12:39
0:12:39
 0:08:20
0:08:20
 0:17:38
0:17:38