filmov
tv
What Does the Gradient Vector Mean Intuitively?
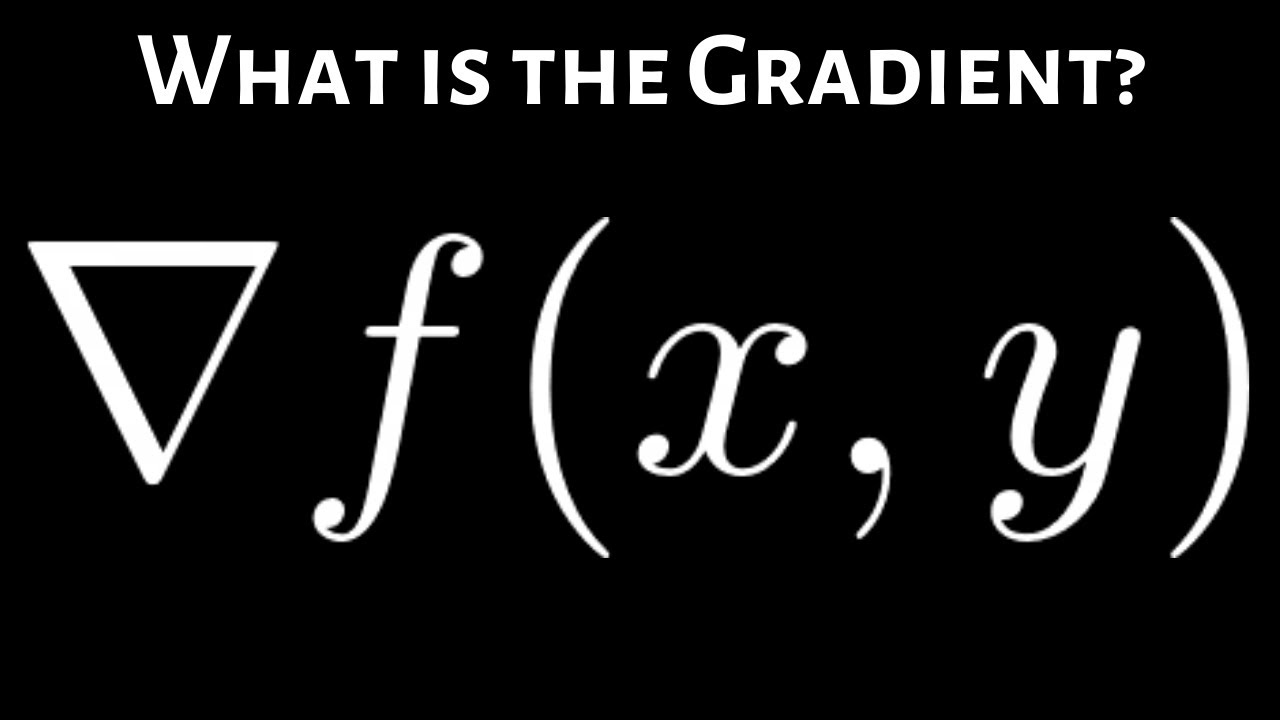
Показать описание
What Does the Gradient Vector Mean Intuitively?
If you enjoyed this video please consider liking, sharing, and subscribing.
You can also help support my channel by becoming a member
Thank you:)
If you enjoyed this video please consider liking, sharing, and subscribing.
You can also help support my channel by becoming a member
Thank you:)
What Does the Gradient Vector Mean Intuitively?
Geometric Meaning of the Gradient Vector
The Gradient Vector Field
Gradient
Gradients and Partial Derivatives
How To Find The Directional Derivative and The Gradient Vector
What is a gradient? Explained in under one minute
Partial Derivatives and the Gradient of a Function
Summary of Vector Derivative Operations and Formulation in Cylindrical and Spherical Coordinates
What is Gradient? #calculus
The Gradient Vector: A Geometric Approach
Facts about the Gradient Vector
The Gradient Vector - Notation and Definition
Why the gradient is the direction of steepest ascent
The Gradient Operator in Vector Calculus: Directions of Fastest Change & the Directional Derivat...
Divergence and curl: The language of Maxwell's equations, fluid flow, and more
Directional Derivatives | What's the slope in any direction?
Geometric Intuition Gradient Vector
Proof of Why Gradient of a Function is Perpendicular to its Level Curves
Visualizing Directional Derivatives and the Gradient
261.10.6 Recap: What Does a Gradient Vector ∇f(x,y) Tell Us?
Oxford Calculus: Gradient (Grad) and Divergence (Div) Explained
Properties of the Gradient Vector
Multivariable Differentiation Lecture 2 Part 5: The Gradient Vector
Комментарии
 0:02:14
0:02:14
 0:14:51
0:14:51
 0:02:18
0:02:18
 0:05:31
0:05:31
 0:05:24
0:05:24
 0:28:30
0:28:30
 0:00:49
0:00:49
 0:10:57
0:10:57
 0:15:06
0:15:06
 0:00:58
0:00:58
 0:17:28
0:17:28
 0:09:47
0:09:47
 0:02:13
0:02:13
 0:10:32
0:10:32
 0:15:04
0:15:04
 0:15:42
0:15:42
 0:12:01
0:12:01
 0:08:37
0:08:37
 0:07:32
0:07:32
 0:04:23
0:04:23
 0:02:48
0:02:48
 0:28:09
0:28:09
 0:05:27
0:05:27
 0:09:32
0:09:32