filmov
tv
This Shouldn't Exist
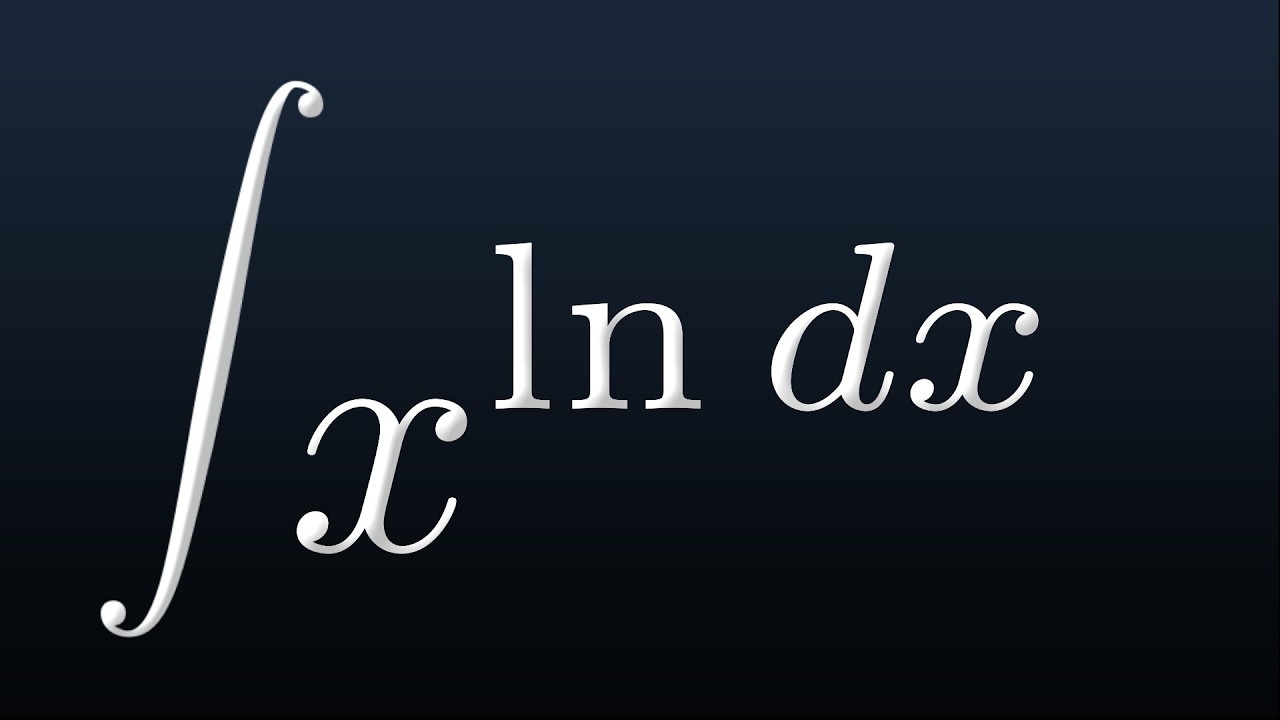
Показать описание
🙏Support me by becoming a channel member!
#math #brithemathguy
This video was sponsored by Brilliant.
Disclaimer: This video is for entertainment purposes only and should not be considered academic. Though all information is provided in good faith, no warranty of any kind, expressed or implied, is made with regards to the accuracy, validity, reliability, consistency, adequacy, or completeness of this information. Viewers should always verify the information provided in this video by consulting other reliable sources.
The ancient computer that simply shouldn't exist
This Shouldn't Exist In Egypt - The Ancient Osirion And Logic Defying Hydraulic Technology
Egypt's Ancient Osirion Pit And Logic Defying Hydraulic Technology That Can't Be Explained...
Gömböc—The Shape That Shouldn't Exist
This Cave Shouldn't Exist
Scientists Discovered An Ancient Civilization Frozen In Ice That Shouldn't Exist
Antikythera Mechanism: The ancient 'computer' that simply shouldn't exist - BBC REEL
This Product Shouldn't Exist
Africa: The Jungle|| That Shouldn't Exist #sorts
the desire to simply not exist
Black Hole Star – The Star That Shouldn't Exist
Why Shouldn't The Universe Exist?
Archaeological Finds That Shouldn’t Exist
Sprunki Reacts to ALL SPRUNKI SUS MODS... | Sprunki Mods that Shouldn't Exist...
But If Dinosaurs Don’t Exist…
This Virus Shouldn't Exist (But it Does)
This $2,000 PC Case SHOULDN'T Exist
Ruxley - this song should not exist (Official Lyric Video)
Sprunki Mods that SHOULD NOT EXIST..
5 Weird Jobs That Don't Exist Anymore 😳
Another Dumb Thing That Shouldn't Exist
The Desire to Not Exist
Ancient Artifacts that shouldn’t exist
THINGS THAT SHOULDN'T EXIST!😳
Комментарии
 0:14:43
0:14:43
 0:11:47
0:11:47
 0:59:37
0:59:37
 0:05:02
0:05:02
 0:12:37
0:12:37
 1:07:17
1:07:17
 0:06:54
0:06:54
 0:01:00
0:01:00
 0:00:15
0:00:15
 0:05:01
0:05:01
 0:09:57
0:09:57
 0:56:51
0:56:51
 0:27:47
0:27:47
 0:09:01
0:09:01
 0:00:57
0:00:57
 0:09:34
0:09:34
 0:11:02
0:11:02
 0:03:02
0:03:02
 0:14:49
0:14:49
 0:00:38
0:00:38
 0:00:42
0:00:42
 0:16:47
0:16:47
 0:00:59
0:00:59
 0:00:24
0:00:24