filmov
tv
3.1.5 Boundary Conditions and Uniqueness Theorems

Показать описание
Given some boundary conditions, do we have enough to find exactly 1 solution? For Laplace's Equation, if we have the boundaries of a region specified, we have exactly one solution inside the region.
3.1.5 Boundary Conditions and Uniqueness Theorems
The Big Theorem of Differential Equations: Existence & Uniqueness
Uniqueness Theorems in Electrostatics | Laplace and Poisson Equation
Boundary conditions and the uniqueness theorems
3.1.6 Conductors and the Second Uniqueness Theorem
Existence & Uniqueness Theorem, Ex1
Boundary Conditions and Uniqueness Theorems
Poisson's & Laplace's equation and Proof of Uniqueness theorem
Uniqueness theorem for Poisson's equation
Existence and uniqueness of boundary-value problems
Find the Interval That a Linear First Order Differential Equation Has a Unique Solution
Uniqueness: The Physics Problem That Shouldn't Be Solved
Existence & Uniqueness of Solutions | Numericals | Higher Order Differential Equations | Maths
Boundary Value Problem (Boundary value problems for differential equations)
Differential equations, a tourist's guide | DE1
Uniqueness proof for Laplace equation (or Poisson equation), Dirichlet problem
Boundary Conditions for Electric Field: Derivations and Explanations
Existence & Uniqueness Theorem, Ex3.5
Intro to Differential Equations - 1.6 - Boundary Value Problem, Existence of a Unique Solution
LEC 26 Uniqueness Theorem for charge free region | HC VERMA | GDS K S
Uniqueness Theorem for First Order DEs
How to determine the general solution to a differential equation
Existence and Uniqueness Theorem for Higher-Order Linear DE
Proving Green's Identity and Second Uniqueness Theorem Problems 1-61c and 3.5
Комментарии
 0:08:37
0:08:37
 0:12:22
0:12:22
 0:04:46
0:04:46
 0:12:16
0:12:16
 0:14:48
0:14:48
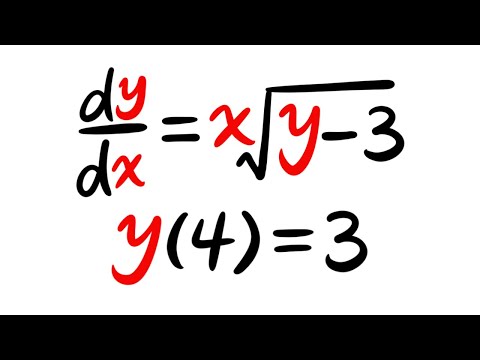 0:11:22
0:11:22
 0:20:27
0:20:27
 0:18:59
0:18:59
 0:14:19
0:14:19
 0:18:02
0:18:02
 0:08:57
0:08:57
 0:12:04
0:12:04
 0:13:15
0:13:15
 0:05:02
0:05:02
 0:27:16
0:27:16
 0:17:22
0:17:22
 0:19:15
0:19:15
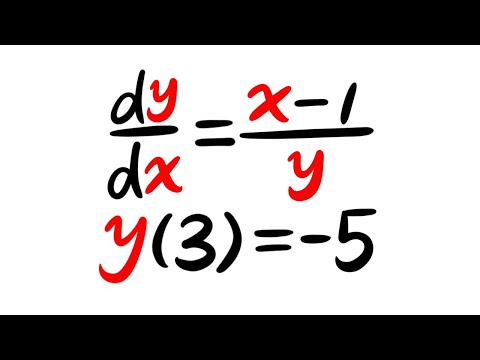 0:07:12
0:07:12
 0:09:27
0:09:27
 0:23:48
0:23:48
 0:11:14
0:11:14
 0:02:03
0:02:03
 0:11:30
0:11:30
 0:39:46
0:39:46