Uniqueness: The Physics Problem That Shouldn't Be Solved

The Uniqueness Theorem can PROVE that this problem only has one possible solution... so however we can find it (e.g. guessing), we know we've got the right one!

In this video, we'll be taking a look at how this uniqueness theorem is derived for the Poisson and Laplace equations in electrostatics.

To begin with, we'll recall what an electric field and potential field are in electrostatics. The electric field is a vector field generated by charged objects. It tells us about the forces experienced by other charged objects placed in the field. A potential field is a scalar field that also gives us similar information. In fact, the gradient operator applied to the potential field gives us (the negative of) the electric field!

Both the electric and potential fields follow Poisson's equation for electrostatics, if they are to obey the laws of physics. This equation relates the divergence of the gradient of the potential field, to the charge density in any region of space we want to study.

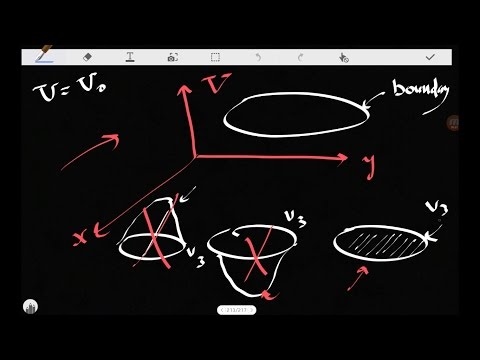
If we consider a particular region of space, such as a sphere, we can simplify our discussion if we assume there are no charges in this region. With this assumption, the charge density becomes zero and the Poisson Equation becomes the Laplace Equation. Also, we can assume we already know the potential values at the surface of our region of space since we measured them. (The potential field is the same as the voltage that we use when talking about electric circuits). The measured potential values make up our "boundary conditions".

At this point, we want to calculate what the potential field is everywhere in our region of space, and we know it must satisfy the boundary conditions (i.e. be the same as our measured values on the boundary).

We can now assume that there are two solutions that are different within our region of space, but the same on the boundary. And then we can subtract one from another to study a new quantity, which also happens to obey the Laplace equation. Additionally, this new quantity is zero on the boundary since our two assumed solutions matched our measured values on the boundary.

Then we can apply some general vector calculus identities to show that the value of our new quantity must be a constant. But since this value is also zero on the boundary, it therefore must be zero everywhere. In other words, our two assumed solutions must be the same as each other if they are to subtract to be equal to zero. We've just found that it is impossible for there to be two different solutions to our problem.

This theorem is the uniqueness theorem, and shows that there is only one possible solution to this problem. This is useful because it means we don't need to solve the problem exactly to figure out the right solution for our scenario. Even if we can GUESS the solution, and then plug it back in to our equations to check that it works, this is ok. The reason is that if we somehow find the solution, we know that it's the only possible one - so we've not accidentally found a solution that works, but doesn't apply to our scenario!

Many of you have asked about the stuff I use to make my videos, so I'm posting some affiliate links here! I make a small commission if you make a purchase through these links.

Thanks so much for watching - please do check out my socials here:
Instagram - @parthvlogs
Music Chanel - Parth G's Shenanigans

Timestamps:
0:00 - The Problem That Only Has One (Guessable) Solution
0:45 - The Electric Field Generated by Charged Objects
2:04 - The Potential Field Generated by Charged Objects
3:05 - The Relationship Between the Potential and Electric Fields
3:45 - The Poisson Equation, Charge Density, and Boundary Conditions
6:05 - The Laplace Equation for Electrostatics (Charge Density = 0)
6:17 - Assuming There Are Two Possible Solutions (V1 and V2)
8:01 - Proving There is Only ONE Possible Solution (V1 = V2)
9:03 - The Uniqueness Theorem, and Why One Solution is Useful - Guesswork!
10:32 - Dirichlet, Neumann, and Mixed Boundary Conditions
10:56 - Summary

[ParthGChannel]

Also, as always do let me know what other topics I should cover on this channel :)

[soorajsahani]

this topic 'Uniqueness theorem" was actually my guess when I saw "when a problem has one solution"

[jennymagnes]

This is the best video I have seen on the uniqueness theorem involving Laplace's equation. Most other videos mix up the boundary conditions for the potential and the potential function itself. Some of the comments disputing your logic forget that the Laplacian only holds for a charge-free region.

[mzshmkn]

holy shit i cant believe why everything sounded familiar it was because this was exactly what i was studying a couple weeks ago in class. amazing!

[petersmythe]

If there's only one configuration inside that produces that configuration on the boundary, then, at least in principle, the boundary contains all of the information of its interior volume... Which means that we've got perfect holographic representation of the field in a 3D space by looking at a 2D boundary of that space.

[pinklinecabs]

Whenever i see your videos not only i get knowledge but to learn more about it.♥

[radiuscubed]

Nice explanation! This literally just came up in my graduate E&M, so this really helped!

[jessstuart]

The reason you must always define a boundary condition is because the classical electric potential blows up to ±∞ at r=0.

[rayeesabdulla]

You are so Good man. thanks a lot.. Thanks a hundred times for this beautiful video.. Which book do you follow to learn these concepts?

[vishalmishra]

*Electric charges also create curvatures in space-time*
Mass curves space-time and is also affected by curvature in space-time. The variation in gravitational potential is modelled as acceleration vector field at any space-time co-ordinate. This is similar to electric field being the negative derivative (gradient) of electric potential. Watch the motion of a charged sphere in an electric field (with no other mass or gravitational field around) to measure the space-time curvature caused by electric field. The resulting motion creates magnetic field, force and magnetic-curvature in space-time. A "more-General" Theory of Relativity (mGR) unifies electro-magnetic force with Gravity from "less-General" Theory of Relativity (lGR) explaining all forces that curve and stretch space-time (and explains how dark-matter curves space-time and dark-energy stretches space-time).

[BrynSCat]

A single static charge is Q.G..to avoid its own collapse it has to exist as a kinetic energy eternal “ER-ER” bride. This avoids singularity & infinity Static charge is its own C.P. inverse. A 3-sphere.(Spinor)Geodesic 90Gly. The speed of light is Path of least action between these symmetries.(between 2 stereographic projection(cos^2) Ep = static charge. Solve the static charge problem in G.R..This is why we see so much duality, we are causality of duality.

[KaliFissure]

Great video as always although I think our convention of charge designation is backwards.

The manifold is lopsided. Gravity says the next moment is more dense than previous. This is why cosmological constant was introduced (before Big Bang also required dark energy and dark matter). The next moment is more dense, this is an inflow, a convergence. The particle that signifies mass is proton so the charge of proton should also be convergent. Electrons have fields which are expansive and repellent filling all of space. Divergent. If there were only one atom of hydrogen in all space the proton would be a point and the electron field would extend to infinity. Negative charge flows towards positive. The future is more dense

[jensphiliphohmann]

04:27f > _...the gradient of the gradient..._
Not rather the divergence of the gradient?

[Sid_R]

Hey Parth, great video as always! However I have a small doubt, I’d appreciate it a lot if you would clarify it.
You mentioned { ∇^2 V = -ρ/ε0 } there, it looked quite similar to gauss law { flux = net charge enclosed/ ε0 } to me. Tell me, does ∇^2 V represent electric flux density?
I should mention, I only understand the topic to the level of high school physics. So please forgive me if I’m speaking nonsense, thanks again. :)

[蒋正-ku]

thanks, this problem appeared in princeton university physics competition

[beaconofwierd]

Does this mean that if you put a huge metal sphere around the earth and measured the potential everywhere on the sphere you could (theoretically) know exactly how all electric charges on earth was distributed? :O

Doesn’t this also mean that we only need 2 dimensions to express charge distribution in 3D :O

[Aritra-MGlacier]

Ok you consider the Dirichlet boundary condition that's why you get V1=V2... On the other hand if you use Neumann's condition you will get V1-V2=constant.

[kushagrac-]

Brother just out of context any tip u wanna give or make a video on it for young ones like me to become a great physicist ??

[Chewbacca]

Hi Parth, you are an inspiration. I am a career changer who is going into education, and I am taking notes on your lecture style. If you can simplify and communicate Poisson's equation for an engineer, it gives me hope said engineer can be as clearly spoken on topics like newtonian mechanics. Thank you for your contributions to science on YouTube.

[lock_ray]

It's surprising how common this "guessing" method is as a foundation for solving differential equations. Though usually you'd have guess a certain family of solutions instead of the specific one.