How to lie using visual proofs

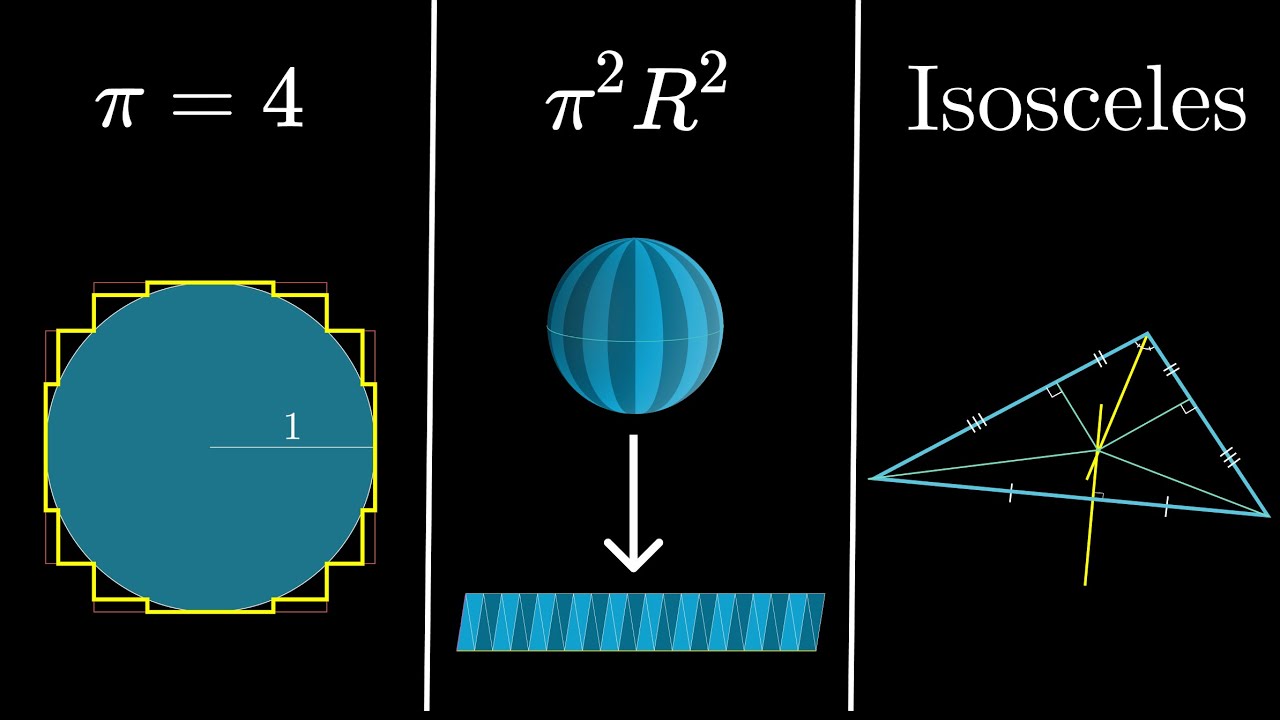
Three false proofs, and what lessons they teach.
An equally valuable form of support is to simply share the videos.

Here's a nice short video on the false pi = 4 proof

Time stamps:
0:00 - Fake sphere proof
1:39 - Fake pi = 4 proof
5:16 - Fake proof that all triangles are isosceles
9:54 - Sphere "proof" explanation
15:09 - pi = 4 "proof" explanation
16:57 - Triangle "proof" explanation and conclusion

Thanks to these viewers for their contributions to translations
French: azerty314159
Portuguese: Wagner K. Martins

------------------

These animations are largely made using a custom python library, manim. See the FAQ comments here:

You can find code for specific videos and projects here:

Music by Vincent Rubinetti.

Download the music on Bandcamp:

Stream the music on Spotify:

------------------

Various social media stuffs:

[QDWhite]

My Calc II prof would always do this. He'd start going through a proof like it was critical to the course and we'd all be furiously copying it off the board. Then he'd get to the 1=2 conclusion at the end and laugh at how none of us saw it coming. Then we'd spend time trying to see where the error was (usually a very well hidden "divide by 0" mistake)

I'll always remember him. He made calculus actually fun and interesting. The world needs more educators like him

[Mutual_Information]

You know you’re a good math communicator when you can lie with proofs.

[HunterJE]

The pi=4 "method" can also be used to "prove " √ 2 = 2 by approximating a diagonal with finer and finer scale taxicab paths

[kipchickensout]

when he drew the triangle and split the base in "two" i was like "wait that's not even close to the middle"

[mCoding]

This is the video mathematicians want to make after being told convergence proofs are "unnecessary details, it's obvious" for the 1000th time. Great work!

[Tutoriala]

As a non-math person who does a lot of CGI work, I’m rather proud of myself for getting the first one right. That sort of warping is something we have to watch out for all the time in UV Unwrapping.
Yay!

[gabiliorcoolkid]

I am a seamstress, an knew from my experience taking 2D shapes to make 3D objects that the "triangles" of the sphere should have a curve. It was very exciting learning the maths behind my empirical knowledge, thank you so much!

[Joe-mvmq]

This was the last video I watched before leaving my aunt's house. This was around 3 months ago, the last conversation I had with her was about my college classes and this math video I watched on YouTube (being you). She passed away roughly a month later and every time I watch this video I get reminded of her. I know you'll never read this comment, but your channel does mean a lot to me and you've helped me learn and nurture my curiosity about mathematics. I don't have any sort of deep statement, I just love these videos and they remind me a lot about days gone by.

Thanks for making these, keep up the good work.

[williamtomlinson]

One of my favorite ways to determine if a statement is plausible is to draw an extreme example. For the triangle proof, I drew a scalene triangle with one very short side. As soon as I tried to connect P, it was obvious it wasn't going to work because the intersection points existed outside of the original triangle.

TL;DR I got three gold stars from Grant and I'm very proud of myself.

[HelixSnake]

I got the third one. I'm usually not smart enough to figure out anything that this channel says is "tricky" by myself so I was really satisfied with that

[tylerbeaumont]

The fact that any circle drawn on a TV will have the same edge length as a square or rectangle which perfectly houses that pixel-based circle is honestly mind boggling. It makes perfect mathematical sense, but at the same time I just can’t wrap my head around it!

Thank you for this enlightening piece of information - I’ll be sure to spread it to random people next time I’m drunk!

[AirPodzol]

Found the flaw. Obviously it was because he assumed that it was a triangle. It was actually just a shape with three angles and three sides.

[codingwizard]

A note on the sphere proof explanation: We can also prove that those "triangles" don't have flat sides by looking at their angles. The dividing lines on the sphere are all perpendicular to the "equator" of the sphere, so each of those triangles would have two right angles.

[benjaminsmith]

I had a SAT prep book way back in the 80s that said whenever the test says "Not drawn to scale", you should immediately redraw it to scale. That rule of thumb has served me well my entire life. Unfortunately, most people will throw out everything they know in the face of a confident deception.

[little_wintry]

I've never been great at math. I barely passed geometry and algebra, and I've never even touched a calculus textbook. But something about your math videos make me feel like I understand it all, it brings back a sort of childlike curiosity where I don't have to feel bad about making mistakes or being wrong, I just get to sit here and learn things. It's oddly soothing for me and I love your videos :)

[The_Jacobian_Hotspot]

It's interesting how the Pi listeners in the animation react when something is noteworthy or thought provoking. I noticed myself understanding better when I saw the pi people understanding together. Very kewl

[mute]

The fun thing about the second "proof", you don't even need to do it with curves. Apply it to a diagonal of a square, and you can "prove" that the square root of 2 equals 2.

[bastienfelix]

There’s something so frustrating about knowing you’re right, but not being able to prove it… good job, magic numbers man, that last example really got me.

[FBI-zbdo]

This channel is absolutely fantastic. Absolutely LOVE you guys! You explain everything very well, and I especially appreciate explanations for the simple terms that I, being a non-native english speaker, don't know from school! Absolutely fantastic stuff!

[ffs]

In 5:57, where 3B1B is drawing, the text in the book says next:
"The point of rigour is not to destroy all intuition; instead it should be used to destroy bad intuition while clarifying and elevating good intuition. It is only with a combination of both rigorous formalism and good intuition that one can tackle complex mathematical problems"
-Terence Tao

"When you yourself are responsible for some new application in mathematics in your chosen field, then your reputation, possibly millions of dollars and long delays in the work, and possibly even human lives, may depend on the results you predict. It is then the need for mathematical rigor will become painfully obvious to you."
-Richard Hamming