filmov
tv
5 easy ways of factoring a trinomial ax^2+bx+c

Показать описание
Learn how to factor a trinomial in ax^2+bx+c when a is not 1, including the AC method, factoring by grouping, the box method, slide and divide, and the tic-tac-toe method. Factoring a trinomial is an important part of your algebra class especially when you need to solve a polynomial equation with a degree 2 or higher. This algebra lesson will help you master your factoring skills for your algebra class. Subscribe to @bprpmathbasics for more math tutorials.
How to use the quadratic formula to factor trinomials: 👉
-----------------------------
-----------------------------
#math #algebra #mathbasics
0:00 Helping you master factoring trinomials
0:09 1st, AC method with grouping
2:08 2nd, AC method with the box
3:35 3rd, AC method, but weird version
4:52 4th, slide & divide
6:33 5th, tic-tac-toe factoring method
How to use the quadratic formula to factor trinomials: 👉
-----------------------------
-----------------------------
#math #algebra #mathbasics
0:00 Helping you master factoring trinomials
0:09 1st, AC method with grouping
2:08 2nd, AC method with the box
3:35 3rd, AC method, but weird version
4:52 4th, slide & divide
6:33 5th, tic-tac-toe factoring method
Factoring Quadratics in 5 seconds! Trick for factorising easily
How To Factor Polynomials The Easy Way!
FASTEST way to factor a trinomial! #shorts
How to Factor and Solve Quadratics - Sneaky Trick - No Fuss Factoring
Factoring 5-term polynomials by grouping
How To Solve Quadratic Equations By Factoring - Quick & Simple! | Algebra Online Course
Factoring Trinomials & Polynomials, Basic Introduction - Algebra
Factoring Quadratics... How? (NancyPi)
We tried 5 easy tricks to save our game | FULL RESULTS
Factoring Trinomials
Learn the ac method for factoring and solving a quadratic equation
Math Antics - Factoring
Factoring completely with a common factor | Algebra 1 | Khan Academy
Whiteboard Math: The Basics of Factoring
Cool Trick for Factoring Numbers
Quickly learn how to factor a quadratic with three terms
Factoring Quadratic Expressions Pt. 1
Factoring 3x³ + x² - 15x - 5 #Shorts #algebra #math #maths #mathematics #education #learn #learning...
How to Factor any Quadratic Equation Easily - Trick for factorising
Quadratic Equations | Solve by factoring | Free Math Videos
Factor Polynomials - Understand In 10 min
Factoring by Grouping Example 😎 #Shorts #algebra #math #maths #mathematics
Box Method of Factoring Trinomials (In Under 2 Minutes)
Factoring - How to Factor Different Types
Комментарии
 0:10:57
0:10:57
 0:11:54
0:11:54
 0:00:55
0:00:55
 0:05:42
0:05:42
 0:05:33
0:05:33
 0:12:29
0:12:29
 0:34:46
0:34:46
 0:09:14
0:09:14
 0:08:56
0:08:56
 0:04:17
0:04:17
 0:05:00
0:05:00
 0:06:18
0:06:18
 0:04:00
0:04:00
 0:08:34
0:08:34
 0:05:42
0:05:42
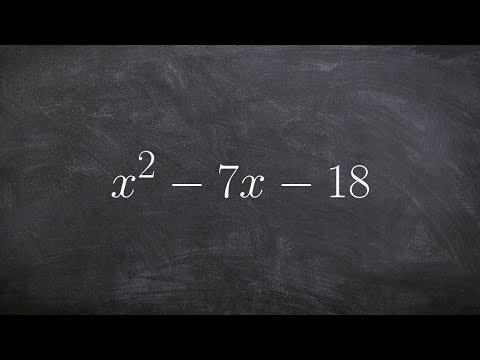 0:01:16
0:01:16
 0:05:53
0:05:53
 0:00:47
0:00:47
 0:06:44
0:06:44
 0:02:43
0:02:43
 0:14:06
0:14:06
 0:00:27
0:00:27
 0:01:36
0:01:36
 0:21:52
0:21:52