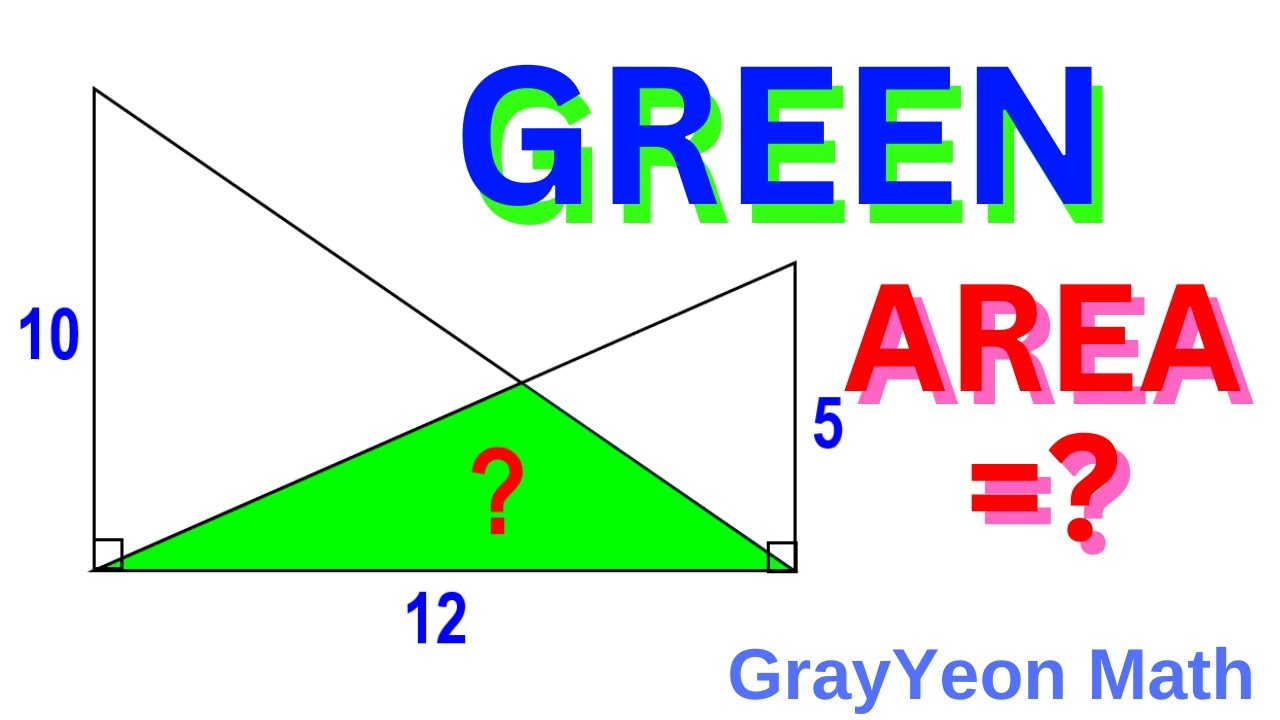
Find the area of the green #geometryskills #mathpuzzles #thinkoutsidethebox

Find the area of the green region

This will be so much appreciated.

#geometryskills #thinkoutsidethebox #mathpuzzles

[Ramkabharosa]

Let O be left bottom vertex and A & B be the two upper vertices. Then the equations
of the lines through O & B and through A& B are y=5x/12 & (y-10)/(0-10)=(x-0)/(12-0).
So 2y=10x/12 & 10-y=10x/12. ∴ 2y=10-y & so 3y=10. ∴ y=10/3= height of the green Δ.
So area of green Δ = (1/2)(base)(height) = (1/2)(12)(10/3) = 2(10) = 20 square units.

[protoss]

1/10 + 1/5 = 1/h
h = 10/3
A = 1/2 (12)(10/3) = 20

[Ramkabharosa]

Let A= Area(left Δ), B= Area(green Δ), and C= Area( right Δ).
Then A+B=60 & B+C=30. From parallel-wall ladder-theorem,
we get 1/B= 1/(A+B) + 1/(B+C)= 1/60 + 1/30=1/20. ∴ B=20.
.

[jimlocke]

Drop a perpendicular from the intersection of the 2 right triangle hypotenuses to the horizontal line segment of length 12. Label its length h. From ratios of sides of similar triangles, h/x=5/12 and h/(12-x)=10/12. Solving the pair of equations, h=10/3. If the horizontal side of the green triangle is considered its base, h is its height and area S=(1/2)(12)(10/3)=20.

My solution is basically the same as harikatragadda's. However, I applied the properties of similar triangles differently to compute the vertical height of the green triangle.

[thorbjrnhellehaven]

I set H to height of green triangle, and X as the left segment of the base line:

Using equal shape:
5/12 = H/X
10/12 = H/(12-X) and 10/12 = 2*(5/12) = (2H)/X
combing:
H/(12-X) = (2H)/X
cross multiplying:
HX = 24H - 2HX
sorting:
3HX = 24H
divide by 3H:
X = 8
insert in first equation:
5/12 = H/8
solving H
H = 40/12

A = (1/2) * 12 * (40/12) = 20

[じーちゃんねる-vn]

The linear ratio of the white triangle on the left to the white triangle on the right is 2:1, so the area ratio is 4:1 60-S:30-S=4:1 ∴S=20

[santiagoarosam]

La relación entre pendientes es 1/2 → Las hipotenusas se cruzan a una distancia de 12/3 desde el extremo derecho → Altura triángulo verde =10/3 → Área verde = 12*(10/3)*(1/2) =20
Gracias y saludos.

[mohamadtaufik]

Green area=0.5*12*10/3=20 square units

[harikatragadda]

If h is the height of S, then by Similarity of the two small right triangles of height h inside S to the large left and right triangles gives
1/h = 1/10 + 1/5 = 3/10
S = ½*h*12 = 20

May I request you to label the figure to make it easy in the comments?

[vinodrajput]

There is simple metho(10×5)÷15=10/3 it is the hight
12×10/3 ×1/2= 20

[himo]

5 : 10 = 1 : 2 1² = 1 2² = 4
area of green region : x
s + x = 5*12/2 = 30 4s + x = 10*12/2 = 60
3s = 30 s = 10 x = 20 area of green region is 20

[Wildcard]

(try before watching)

f1(x)=-(5/6)x+10; f2(x)=(5/12)x
f1(x)=f2(x)
-(5/6)x+10=(5/12)x
(5/4)x=10
x=8
h=f2(8)=(5/12)*8=5*2/3=10/3
A=g*h/2=12*(10/3)/2=20

[tintinfan]

Your answer is wrong...the correct answer is 26.65 square units