filmov
tv
Prove this Trigonometric Identity | Step-by-Step Explanation
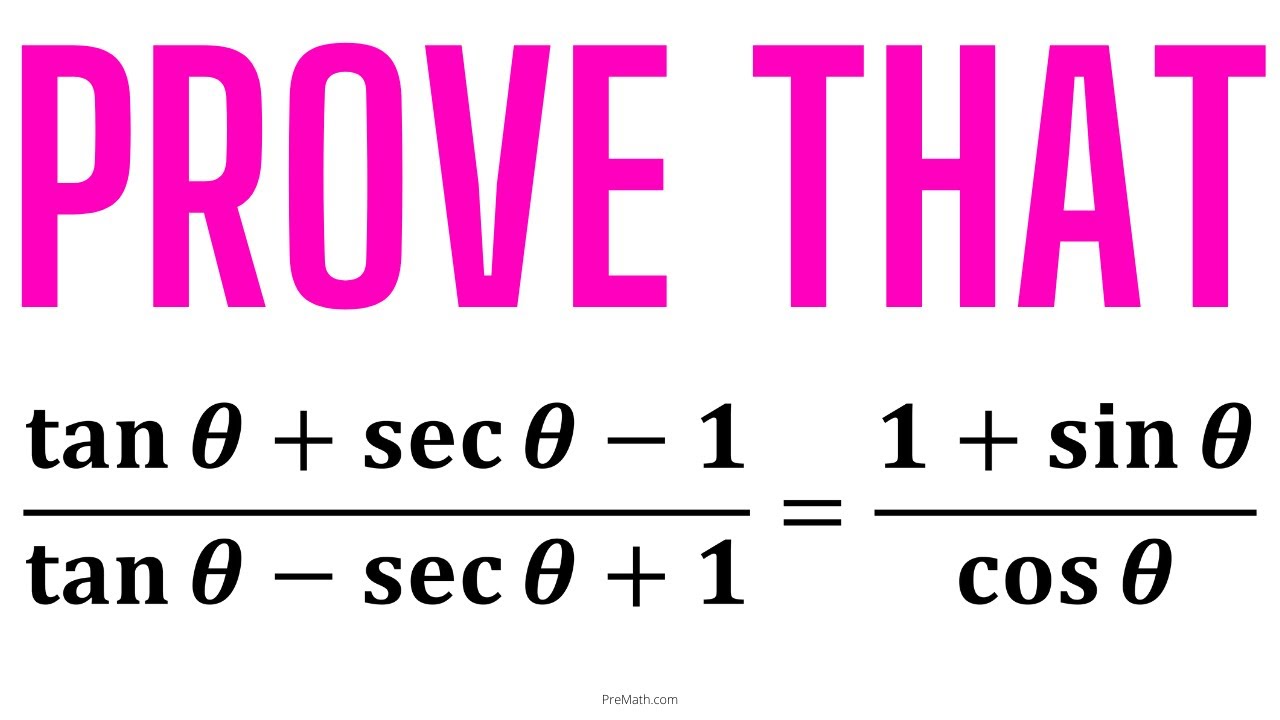
Показать описание
#OlympiadMathematics #OlympiadPreparation #CollegeEntranceExam
Verifying Trigonometric Identities
Learn How To Prove A Trigonometry Question & Apply Trig Identities Effectively
Verifying Trigonometric Identities
How to Prove Trigonometric Identities (and how not to)
Verifying Trigonometric Identities Easily - Strategy Explained (14 Examples)
Prove this Trigonometric Identity | Step-by-Step Explanation
Verifying a trigonometric Identities
Proving Trigonometric Identities Grade 12
Strategy to Prove Trigonometric Identity
Verifying trigonometric identities, hard with multiple steps
Solving Trigonometric Identity EXAMPLE | Pre-Calculus
Prove Trigonometric Identities Getting Started MCR3U
Prove This Trigonometric Identity | Step-by-Step Tutorial
How to Prove Trigonometric Identities (Precalculus - Trigonometry 24)
Trig Identities
The Best Way to Master Trigonometric Identities
a trig identities song???
Solving Trigonometric Identity EXAMPLE | Pre-Calculus
Prove trigonometric identities
Trigonometric identity example proof involving sin, cos, and tan | Introduction to trigonometry
Trig Visualized: One Diagram to Rule them All (six trig functions in one diagram)
Verifying Trigonometric Identities With Double Angle Formulas
Proving Trigonometric Identities | Fundamental Trigonometric Identities | Formulas | Sample Problems
PROVE this Trigonometric Identity | Fast & Easy Tutorial
Комментарии
 0:24:51
0:24:51
 0:13:17
0:13:17
 0:09:14
0:09:14
 0:07:37
0:07:37
 0:25:08
0:25:08
 0:07:23
0:07:23
 0:05:12
0:05:12
 0:05:19
0:05:19
 0:02:39
0:02:39
 0:06:53
0:06:53
 0:00:58
0:00:58
 0:07:57
0:07:57
 0:06:12
0:06:12
 0:55:39
0:55:39
 0:27:57
0:27:57
 0:03:36
0:03:36
 0:00:26
0:00:26
 0:00:55
0:00:55
 0:01:01
0:01:01
 0:03:30
0:03:30
 0:04:15
0:04:15
 0:15:19
0:15:19
 0:13:30
0:13:30
 0:05:17
0:05:17